|
查看: 2707|回复: 23
|
錯了。。。錯了。。。全部錯了。。。(16 Aug更新)
[复制链接]
|
|
|
我放錯題目了。。。之前那題。。。那么簡單。。。不好意思
應該是這題。。。。
arc sin (5/x) + arc sin(12/x) = π/2
求x....
[ 本帖最后由 秋冬雪叶 于 16-8-2009 01:19 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 02:33 PM
|
显示全部楼层
发表于 24-7-2009 02:33 PM
|
显示全部楼层
真的不会。。。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2009 04:17 PM
|
显示全部楼层
发表于 24-7-2009 04:17 PM
|
显示全部楼层
原帖由 秋冬雪叶 于 24-7-2009 02:16 PM 发表 
已知tan^(2) x = 2tan^(2) y + 1
证cos 2x + sin(^)2 y = 0
tan^(2) x = 2tan^(2) y + 1
tan^(2) x + 1 = 2tan^(2) y + 2
sec^(2) x = 2 sec^(2) y
cos^(2) y = 2 cos^(2) x
1 - sin^(2)y = 2 cos^(2) x
2 cos^(2) x - 1 + sin^(2) y = 0
cos 2x + sin^(2) y = 0 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-7-2009 07:10 PM
|
显示全部楼层
原帖由 flash 于 24-7-2009 04:17 PM 发表  tan^(2) x = 2tan^(2) y + 1tan^(2) x + 1 = 2tan^(2) y + 2sec^(2) x = 2 sec^(2) ycos^(2) y = 2 cos^(2) x1 - sin^(2)y = 2 cos^(2) x2 cos^(2) x - 1 + sin^(2) y = 0cos 2x + sin^(2) y = 0 tan^(2) x = 2tan^(2) y + 1tan^(2) x + 1 = 2tan^(2) y + 2sec^(2) x = 2 sec^(2) ycos^(2) y = 2 cos^(2) x1 - sin^(2)y = 2 cos^(2) x2 cos^(2) x - 1 + sin^(2) y = 0cos 2x + sin^(2) y = 0
诶~~~原来如此
多谢前辈指教~~~ |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-8-2009 07:09 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-8-2009 09:34 PM
|
显示全部楼层
发表于 6-8-2009 09:34 PM
|
显示全部楼层
我尝试做了这题,不知道对不对。。。
As 162/18=9 (by inspection)
log24=log(3x8)=a
log3+log8=a
multiply by 2,
2log3+2log8=2a
log9+log64=2a----(1)
Known that log18=b----(2)
(1)+(2) log9+log64+log18=2a+b
so, log9+log18=2a+b-log64
log(9x18)=2a+b-log64
log162=2a+b-log64
我只作到这里,log64没想到要怎样消掉。。。可能那位大大有更好,更正确的解法也说不定。。。
[ 本帖最后由 VernGalaxy 于 6-8-2009 09:45 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-8-2009 11:42 PM
|
显示全部楼层
原帖由 VernGalaxy 于 6-8-2009 09:34 PM 发表  我尝试做了这题,不知道对不对。。。As 162/18=9 (by inspection)log24=log(3x8)=alog3+log8=amultiply by 2,2log3+2log8=2alog9+log64=2a----(1)Known that log18=b----(2)(1)+(2) log9+log64 ... 我尝试做了这题,不知道对不对。。。As 162/18=9 (by inspection)log24=log(3x8)=alog3+log8=amultiply by 2,2log3+2log8=2alog9+log64=2a----(1)Known that log18=b----(2)(1)+(2) log9+log64 ...
可惜。。。。。還差一點答案就出來了。。。。。
不過
也謝謝您了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-8-2009 12:25 PM
|
显示全部楼层
发表于 7-8-2009 12:25 PM
|
显示全部楼层
原帖由 秋冬雪叶 于 24-7-2009 02:16 PM 发表 
已知 log 24 = a log 18 = b
用a,b來表示
log 162......
可以給我看看過程嗎????
謝謝
log 24 = log (8 x 3) = a
3 log 2 + log 3 = a ------(1)
log 18 = log (2 x 9) = b
log 2 + 2 log 3 = b -----(2)
(1) x 2
6 log 2 + 2 log 3 = 2a ----- (3)
(2) x 3
3 log 2 + 6 log 3 = 3b ------(4)
(3) - (2)
5 log 2 = 2a - b
log 2 = (2a - b)/5
(4) - (1)
5 log 3 = 3b - a
log 3 = (3b - a)/5
log 162 = log (81 x 2) = 4 [(3b - a)/5] + (2a - b)/5 = (11b - 2a) / 5
[ 本帖最后由 flash 于 7-8-2009 07:18 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-8-2009 05:22 PM
|
显示全部楼层
原帖由 flash 于 7-8-2009 12:25 PM 发表  log 24 = log (8 x 3) = a3 log 2 + log 3 = a ------(1)log 18 = log (2 x 9) = blog 2 + 2 log 3 = b -----(2)(1) x 26 log 2 + 2 log 3 = 2a ----- (3)(2) x 33 log 2 + 6 log 3 = 3 ... log 24 = log (8 x 3) = a3 log 2 + log 3 = a ------(1)log 18 = log (2 x 9) = blog 2 + 2 log 3 = b -----(2)(1) x 26 log 2 + 2 log 3 = 2a ----- (3)(2) x 33 log 2 + 6 log 3 = 3 ...
啊~~~~~
原來如此
其實遇到類似的題目我都很頭大
好彩遇到您~~~~
謝謝~~~ |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 8-8-2009 11:49 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-8-2009 12:10 AM
|
显示全部楼层
发表于 9-8-2009 12:10 AM
|
显示全部楼层
你的题目是 y = tan x° 吧!
x° = x° · π/180° = πx/180
dy/dx
= dtan x°/dx
= dtan(πx/180)/dx
= sec²(πx/180) · π/180
= (π/180) sec²(πx/180)
= (π/180) sec² x° |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 9-8-2009 10:52 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-8-2009 08:50 PM
|
显示全部楼层
发表于 9-8-2009 08:50 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 9-8-2009 09:20 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-8-2009 12:01 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-8-2009 12:49 PM
|
显示全部楼层
发表于 10-8-2009 12:49 PM
|
显示全部楼层
∫[(2x-1) √(x+2)] dx
Let u = x + 2
x = u – 2
dx/du = 1
∫(2u – 5)( √u)du
=∫2u^(3/2) – 5u^(1/2) du
=(4/5)u^(5/2) – (10/3)u^(3/2) + c
=u^(3/2)(4u/5 – 10/3)
=(x + 2)^(3/2) [(4/5)*(x + 2) – (10/3)]
不懂对不对  |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-8-2009 01:16 PM
|
显示全部楼层
原帖由 DADDY_MUMMY 于 10-8-2009 12:49 PM 发表  ∫[(2x-1) √(x+2)] dxLet u = x + 2x = u – 2dx/du = 1∫(2u – 5)( √u)du=∫2u^(3/2) – 5u^(1/2) du=(4/5)u^(5/2) – (10/3)u^(3/2) + c=u^(3/2)(4u/5 – 10/3)=(x + 2)^(3/2) [(4/5)*(x + 2) ... ∫[(2x-1) √(x+2)] dxLet u = x + 2x = u – 2dx/du = 1∫(2u – 5)( √u)du=∫2u^(3/2) – 5u^(1/2) du=(4/5)u^(5/2) – (10/3)u^(3/2) + c=u^(3/2)(4u/5 – 10/3)=(x + 2)^(3/2) [(4/5)*(x + 2) ...
您做對了!!!!
謝謝~~~
[ 本帖最后由 秋冬雪叶 于 10-8-2009 01:38 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-8-2009 03:16 PM
|
显示全部楼层
发表于 10-8-2009 03:16 PM
|
显示全部楼层
不要放我的名字,我会害羞的。  |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-8-2009 11:23 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-8-2009 09:44 PM
|
显示全部楼层
发表于 13-8-2009 09:44 PM
|
显示全部楼层
用打字有点麻烦。。。拍了作业,不过不是很清,抱歉。
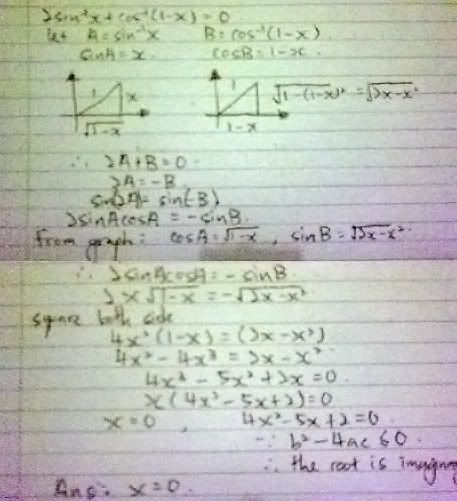
ans:x=0? |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|