|
|
 发表于 11-2-2006 01:35 PM
|
显示全部楼层
发表于 11-2-2006 01:35 PM
|
显示全部楼层
(i)的最后一步是 >= (2m+1)^2/(2m+1)^2 = 1 因为 AM-HM里
(a+b+c)/3 >= 3/(1/a + 1/b + 1/c) <=> a+b+c >= 9/(1/a + 1/b + 1/c)
(ii) 的名字叫 Jensen ,不是cauchy 
不过两个都对了! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-2-2006 03:13 PM
|
显示全部楼层
发表于 13-2-2006 03:13 PM
|
显示全部楼层
證明 x^4 + 11/x > 10
[ 本帖最后由 hamilan911 于 13-2-2006 03:36 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-2-2006 03:29 PM
|
显示全部楼层
发表于 13-2-2006 03:29 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-2-2006 06:23 PM
|
显示全部楼层
发表于 13-2-2006 06:23 PM
|
显示全部楼层
闪亮三兄弟不等式 (乱掰的) (乱掰的)
已知 a+b+c=3 且 a,b,c>0 证明
(i)a^2/(b+1) + b^2/(c+1) + c^2/(a+1) >= 3/2
(ii) a/(b+1) + b/(c+1) + c/(a+1) >= 3/2
(iii)a/(b^2+1) + b/(c^2+1) + c/(a^2+1) >= 3/2

* (iii) 的不简单!提示:先证明 a/(b^2+1) >= a - ab/2 .... 然后证明 ab+ac+bc =< 3 ...
[ 本帖最后由 dunwan2tellu 于 13-2-2006 06:36 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-2-2006 05:10 PM
|
显示全部楼层
发表于 15-2-2006 05:10 PM
|
显示全部楼层
(i)用cauchy
(b+1+c+1+a+1)[(a^2)/(b+1) + (b^2)/(c+1) + (c^2)/(a+1)] >= (a+b+c)^2
[(a^2)/(b+1) + (b^2)/(c+1) + (c^2)/(a+1)] >= 3^2 / (3+3)
[(a^2)/(b+1) + (b^2)/(c+1) + (c^2)/(a+1)] >= 3/2
(ii)
已知 a^2 + b^2 + c^2 >= ab + bc + ac
(a+b+c)^2 >= 3(ab + bc + ac)
ab + bc + ac =< 3
[a(b+1)+b(c+1)+a(c+1)][a/(b+1) + b/(c+1) + c/(a+1)] >= (a+b+c)^2
[a(b+1)+b(c+1)+a(c+1)] =< 6
[a/(b+1) + b/(c+1) + c/(a+1)] >= 3^2 / 6
[a/(b+1) + b/(c+1) + c/(a+1)] >= 3/2
(iii)
-b(b-1)^2 =< 0
-b^3 + 2b^2 - b + 2 - 2 =< 0
(2-b)/2 =< 1/(b^2 + 1)
a/(b^2 + 1) >= a - ab/2
a/(b^2+1) + b/(c^2+1) + c/(a^2+1) >= a+b+c - (ab+bc+ac)/2
a/(b^2+1) + b/(c^2+1) + c/(a^2+1) >= 3 - 3/2
a/(b^2+1) + b/(c^2+1) + c/(a^2+1) >= 3/2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-2-2006 03:24 PM
|
显示全部楼层
发表于 16-2-2006 03:24 PM
|
显示全部楼层
对了。
再来一对双胞胎不等式!
(i)若a,b>0 , a+b=1 证明:
(a+ 1/a)(b + 1/b)>= 25/4
(ii) 若 a,b,c>0 , a+b+c=1 证明
(a+ 1/a)(b+ 1/b)(c+ 1/c)>= 1000/27 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-2-2006 09:44 PM
|
显示全部楼层
发表于 16-2-2006 09:44 PM
|
显示全部楼层
(i)
用AM-GM
a + 1/(4a) >= 1
(a+b)/2 >= sqrt{ab} -> ab =< 1/4 1/ab >= 4
a + 1/a = a + 1/(4a) + 3/(4a) >= 1 + 3/(4a)
b + 1/b = a + 1/(4b) + 3/(4b) >= 1 + 3/(4b)
(a+1/a)(b+1/b) >= [1 + 3/(4a)][1 + 3/(4b)]
>= 1 + 3/4 (1/a + 1/b) + 9/(16ab)
>= 1 + 3(4)/4 + 9(4)/16
>= 25/4
(ii)
用AM-GM
a + 1/(9a) >= 2/3
(a+b+c)/3 >= cbrt{abc} -> abc =< 1/27 1/abc >= 27
(1/a + 1/b + 1/c)/3 >= cbrt{1/abc}
1/a + 1/b + 1/c >= 9
a + 1/a = a + 1/(9a) + 8/(9a) >= 2/3 + 8/(9a)
b + 1/b = b + 1/(9b) + 8/(9b) >= 2/3 + 8/(9b)
c + 1/c = c + 1/(9c) + 8/(9c) >= 2/3 + 8/(9c)
(a + 1/a)(b + 1/b)(c + 1/c) >= [2/3 + 8/(9a)][2/3 + 8/(9b)][2/3 +8/(9b)]
>= 8/27 + 32/81 (1/a + 1/b + 1/c) + 128/243 (1/ab + 1/bc + 1/ac) + 512/729abc
>= 8/27 + 32(9)/81 + 128(27)/243 + 512(27)/729
>= 1000/27 Q.E.D |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-2-2006 03:38 PM
|
显示全部楼层
发表于 17-2-2006 03:38 PM
|
显示全部楼层
原帖由 hamilan911 于 16-2-2006 09:44 PM 发表
(i)
用AM-GM
a + 1/(4a) >= 1
(a+b)/2 >= sqrt{ab} -> ab =< 1/4 1/ab >= 4
a + 1/a = a + 1/(4a) + 3/(4a) >= 1 + 3/(4a)
b + 1/b = a + 1/(4b) + 3/(4b) >= 1 + 3/(4b)
(a+ ...
我们也可以找他的通项
若 a1,a2,...,an >0 且 a1+a2+...+an = 1
证明 :
(a1 + 1/a1)(a2 + 1/a2)...(an + 1/an) >= (n + 1/n)^2
*p/s : 刚刚看到Jensen 可以用。呵呵!
[ 本帖最后由 dunwan2tellu 于 17-2-2006 03:40 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-2-2006 12:00 AM
|
显示全部楼层
发表于 19-2-2006 12:00 AM
|
显示全部楼层
原帖由 hamilan911 于 16-2-2006 09:44 PM 发表
(i)
用AM-GM
a + 1/(4a) >= 1
(a+b)/2 >= sqrt{ab} -> ab =< 1/4 1/ab >= 4
a + 1/a = a + 1/(4a) + 3/(4a) >= 1 + 3/(4a)
b + 1/b = a + 1/(4b) + 3/(4b) >= 1 + 3/(4b)
(a+ ...
我们也有 a + 1/a >= 25/4(3a+1) <==> (2a-1)^2(3a+4) >= 0
所以 LHS=(a + 1/a)(b +1/b) >= (25/4)^2 * 1/(3a+1)(3b+1)
不过 {(3a+1)+(3b+1)}/2 >= sqrt{(3a+1)(3b+1)} <==>25/4 >={(3a+1)(3b+1)}
所以 LHS >= (25/4)^2 (4/25) = 25/4  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-2-2006 08:07 PM
|
显示全部楼层
发表于 19-2-2006 08:07 PM
|
显示全部楼层
根号不等式:
a,b,c>0 ,证明
sqrt{(ab+ac+bc)/3} =< cbrt{[(a+b)(a+c)(b+c)]/8}
*提示:先证明 9(a+b)(a+c)(b+c) >= 8(a+b+c)(ab+ac+bc)
[ 本帖最后由 dunwan2tellu 于 21-2-2006 07:30 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-2-2006 05:14 PM
|
显示全部楼层
发表于 24-2-2006 05:14 PM
|
显示全部楼层
hamilan911 , 怎么不来玩不等式啦?哈哈。
题目:
(i)a,b,c>0 ,证明
1/(a^3+b^3+abc) + 1/(a^3+c^3+abc) +1/(b^3+c^3+abc) =< 1/abc
(ii) a,b,c,d >0 , abcd=1 证明
sum (1/(a^4+b^4+c^4 +1)) =< 1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-2-2006 08:06 PM
|
显示全部楼层
发表于 28-2-2006 08:06 PM
|
显示全部楼层
schur inequality
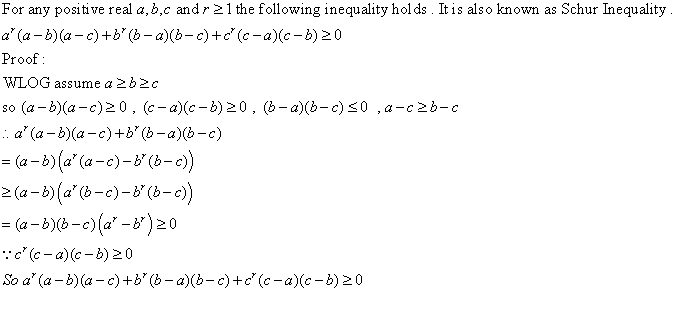
通常 r = 1 时,
a^3 + b^3 + c^3 + 3abc >= a^2(b+c) + b^2(a+c)+c^2(a+b)
一般来说,它比 AM-GM 强很多!
[ 本帖最后由 dunwan2tellu 于 28-2-2006 08:07 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-3-2006 05:44 PM
|
显示全部楼层
发表于 3-3-2006 05:44 PM
|
显示全部楼层
题目:
(i)证明 a^3/(a^2+b^2) >= a - b/2 , for all a,b>0 .
(ii)已知 a+b+c = 1 , a,b,c>0
证明 a^3/(a^2+b^2) + b^3/(b^2+c^2)+c^3/(c^2+a^2) >= 1/2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 8-3-2006 08:32 PM
|
显示全部楼层
发表于 8-3-2006 08:32 PM
|
显示全部楼层
题目:
对于所有正实数 a_i , 我们有 a1 + a2 + a3 + ... + an = 1 ( n 是自然数)
证明不等式
(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an) >= (n + 1)^n
* 简单,只用 am-gm-hm
[ 本帖最后由 dunwan2tellu 于 8-3-2006 09:40 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-3-2006 03:44 PM
|
显示全部楼层
发表于 9-3-2006 03:44 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 3-3-2006 05:44 PM 发表
题目:
(i)证明 a^3/(a^2+b^2) >= a - b/2 , for all a,b>0 .
(ii)已知 a+b+c = 1 , a,b,c>0
证明 a^3/(a^2+b^2) + b^3/(b^2+c^2)+c^3/(c^2+a^2) >= 1/2
a^3/(a^2 + b^2) - (2a - b)/2
= [2a^3 - (2a^3 +2ab^2 -a^b -b^3)]/2(a^2 + b^2)
= b(b -a)^2 /2(a^2 + b^2) >=0 (a,b>0)
所以a^3/(a^2+b^2) >= a - b/2
a^3/(a^2+b^2) + b^3/(b^2+c^2)+c^3/(c^2+a^2) >= a - b/2 + b - c/2 + c - a/2
>= (a+b+c) - (a+b+c)/2
>= 1/2 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-3-2006 04:15 PM
|
显示全部楼层
发表于 9-3-2006 04:15 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 24-2-2006 05:14 PM 发表
hamilan911 , 怎么不来玩不等式啦?哈哈。
题目:
(i)a,b,c>0 ,证明
1/(a^3+b^3+abc) + 1/(a^3+c^3+abc) +1/(b^3+c^3+abc) =< 1/abc
(ii) a,b,c,d >0 , abcd=1 证明
sum (1/(a^4+b^4+c^4 ...
(i)已知a^3 + b^3 >= ab(a+b)
b^3 + c^3 >= bc(b+c)
c^3 + a^3 >= ca(c+a)
1/(a^3+b^3+abc) + 1/(a^3+c^3+abc) +1/(b^3+c^3+abc)
=< 1/ab(a+b+c) + 1/ac(a+b+c) + 1/bc(a+b+c)
=< 1/abc
(ii)已知a^4 +b^4 +c^4 >= abc(a+b+c)
sum(1/(a^3+b^3+c^3+1)) =< sum((1/abc(a+b+c+d))
=< 1/abcd
=< 1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-3-2006 04:26 PM
|
显示全部楼层
发表于 9-3-2006 04:26 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 8-3-2006 08:32 PM 发表
题目:
对于所有正实数 a_i , 我们有 a1 + a2 + a3 + ... + an = 1 ( n 是自然数)
证明不等式
(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an) >= (n + 1)^n
* 简单,只用 am-gm-hm
[(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an)]^(1/n) >= n/sum(a1/(a1+1))
a1/(a1+1) = 1 - 1/(a1+1)
[sum(1/(a1+1))]/n >= n/(sum(a1) + n)
>= n/(1+n)
sum(1/(a1+1)) >= n^2/(1+n)
sum(a1/(a1+1)) = sum(1 - 1/(a1+1))
= n - sum(1/(a1+1))
=< n - n^2/(1+n)
=< n/(1+n)
[(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an)]^(1/n) >= n/(n/(1+n))
>= n+1
(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an) >= (n+1)^n
[ 本帖最后由 hamilan911 于 9-3-2006 08:45 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-3-2006 05:44 PM
|
显示全部楼层
发表于 9-3-2006 05:44 PM
|
显示全部楼层
原帖由 hamilan911 于 9-3-2006 04:26 PM 发表
[(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an)]^(1/n) >= n/sum(a1/(a1+1))
a1/(a1+1) = 1 - 1/(a1+1)
[sum(1/(a1+1))]/n >= n/(sum(a1) + n)
>= n/(1+n)
sum (a1/(a1+1)) =< n - n^2/(1+n)
=< n/(1+n)
[(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an)]^(1/n) >= n/(n/(1+n)
>= n+1
(1 + 1/a1)(1 + 1/a2)(1 + 1/a3)...(1 + 1/an) >= (n+1)^n
对了!
哈哈。试看其他的吧!
[ 本帖最后由 dunwan2tellu 于 9-3-2006 08:46 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-3-2006 05:28 PM
|
显示全部楼层
发表于 11-3-2006 05:28 PM
|
显示全部楼层
来两题较简单的
(i)a,b,c>0 且 abc=1 求证
sqrt{(1+a^2)/(c+ab)}+ sqrt{(1+b^2)/(a+bc)} + sqrt{(1+c^2)/(b+ac)}>= 3
(ii) a,b >0 求证
1/(a^2 + ab + b^2) + 1/(a^2 + a + 1) + 1/(b^2 + b + 1) =< 1/3 * ( 1/a + 1/b + 1/ab )
 
[ 本帖最后由 dunwan2tellu 于 11-3-2006 05:56 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-3-2006 05:55 PM
|
显示全部楼层
发表于 11-3-2006 05:55 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 11-3-2006 05:28 PM 发表
来两题较简单的
(i)a,b,c>0 且 abc=1 求证
sqrt{(1+a^2)/(c+ab)}+ sqrt{(1+b^2)/(a+bc)} + sqrt{(1+c^2)/(b+ac)}>= 3
(ii) a,b,c >0 求证
1/(a^2 + ab + b^2) + 1/(a^2 + a + 1) + 1/(b^2 + ...
(i)(1+a^2)/(c+ab) = c(1+a^2)/(1+c^2)
用AM-GM
[sqrt{(1+a^2)/(c+ab)}+ sqrt{(1+b^2)/(a+bc)} + sqrt{(1+c^2)/(b+ac)}]/3
>= [sqrt{abc}]^(1/3)
所以sqrt{(1+a^2)/(c+ab)}+ sqrt{(1+b^2)/(a+bc)} + sqrt{(1+c^2)/(b+ac)}>= 3
(ii)已知a^2 + b^2 >= 2ab
a^2 + ab + b^2 >= 3ab
1/(a^2 + ab + b^2) =< 1/(3ab)
a^2 + 1 >= 2a
a^2 + a + 1 >= 3a
1/(a^2 + a + 1) >= 1/(3a)
1/(a^2 + ab + b^2) + 1/(a^2 + a + 1) + 1/(b^2 + b + 1) =< 1/3 *(1/a +1/b +1/ab)
[ 本帖最后由 hamilan911 于 11-3-2006 06:09 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|