初等不等式训练(题目在第1页)

dunwan2tellu

pipi 于 28-6-2005 09:25 AM  说 :
对于第22题，这里有个另类的解法，有点＂神奇＂

的却有点神奇。没想到还可以利用 cosA=<1 来下手 。



请 证 明 sinA + sinB + sinC > 2  , A , B , C  都 是 锐 角  且  是 三 角 形  内 角



[ Last edited by dunwan2tellu on 29-6-2005 at 02:39 PM ]

pipi

dunwan2tellu 于 28-6-2005 02:10 PM  说 :
请 证 明 sinA + sinB + sinC > 2  , A , B , C  为  三 角 形  内 角。

有问题！！！
counterexample:
A = 1
B = 1
C = 178
(units are in degree)

dunwan2tellu

pipi 于 29-6-2005 10:39 AM  说 :

有问题！！！
counterexample:
A = 1
B = 1
C = 178
(units are in degree)

Ermm ...  我 想 A , B , C  都 必 须  是  锐 角  才 行

题 目 更 改

[ Last edited by dunwan2tellu on 29-6-2005 at 02:40 PM ]

pipi

dunwan2tellu 于 28-6-2005 02:10 PM  说 :
请 证 明 sinA + sinB + sinC > 2  , A , B , C  都 是 锐 角  且  是 三 角 形  内 角

我会试试的。。。
哈！哈！看来网友们不太喜欢不等式。。。
不要紧，我自得其乐
再来玩玩：

灰羊

我肥來了!!!
29題

33題


[ Last edited by 灰羊 on 30-6-2005 at 07:19 PM ]

dunwan2tellu

我也来玩玩



31)   左 两 个 是AM-GM  ,  右 两 个 是 GM-HM

32) 曾 看 过 个  美 的 解 法 ，
设 左 式 为 P ，  右 式 为 Q ，   发 现  2P + Q = 1 .   
解 得 Q>=1  后 用 P = 1/2 (1-Q)  来 解 P .



[ Last edited by dunwan2tellu on 1-7-2005 at 05:33 PM ]

dunwan2tellu

这里有几题不等试，来试试吧 ！





[ Last edited by dunwan2tellu on 5-7-2005 at 03:37 PM ]

灰羊

dunwan2tellu 于 30-6-2005 20:26  说 :
我也来玩玩



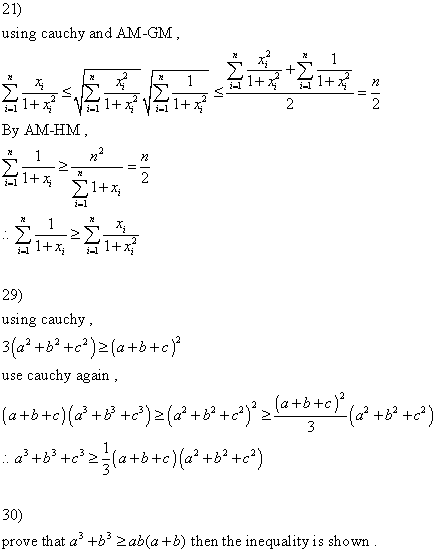
31)   左 两 个 是AM-GM  ,  右 两 个 是 GM-HM

32) 曾 看 过 个  美 的 解 法 ，
设 左 式 为 ...

32應該使用第一頁的排序不等式
可是我看不明什麼是a'..........

铁蛋

大家试试！

如果 a,b,c > 0 ; abc = 1，证不等式



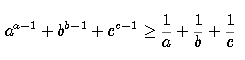
[ Last edited by 铁蛋 on 4-7-2005 at 11:49 AM ]

dunwan2tellu

灰羊 于 3-7-2005 06:27 PM  说 :

32應該使用第一頁的排序不等式
可是我看不明什麼是a'..........

要 解 Q >=1 ,  只 需  注 意 到 2bc =< b^2 + c^2  ....

a_i '   是 a_i  的  排 序 。   好 比 a_1 = 1 , a_2 = 10  那 么  他 的  另 个  排 序  是 a_1' = 10  , a_2 ' = 1  。

灰羊

dunwan2tellu 于 4-7-2005 15:51  说 :



要 解 Q >=1 ,  只 需  注 意 到 2bc =< b^2 + c^2  ....

a_i '   是 a_i  的  排 序 。   好 比 a_1 = 1 , a_2 = 10  那 么  他 的  另 个  排 序  是 a_1' = 10  , a_2 ' = 1  。

a'是任意的嗎????
a1=1
a2=2
a3=3
a4=4

a1'可以是2,3這樣嗎?

dunwan2tellu

铁蛋 于 4-7-2005 11:48 AM  说 :
大家试试！

如果 a,b,c > 0 ; abc = 1，证不等式

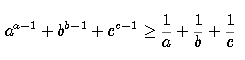
1/a ( a^a) + 1/b (b^b) + 1/c (c^c) >= (1/a+1/b+1/c)(abc)=1/a + 1/b + 1/c

灰羊 于 4-7-2005 09:56 PM  说 :


a'是任意的嗎????
a1=1
a2=2
a3=3
a4=4

a1'可以是2,3這樣嗎?

是 的 ！

[ 本帖最后由 dunwan2tellu 于 14-2-2006 08:57 PM 编辑 ]

铁蛋

[quote] dunwan2tellu 于 5-7-2005 03:04 PM  说 :




谢谢 dunwan2tellu 的解。可是 x + y + z 未必是整数，而 AGM inequality 的条件是 n is integer. 所以这个解只证明了原本问题的一部分。

灰羊

铁蛋 于 5-7-2005 17:19  说 :
[quote] dunwan2tellu 于 5-7-2005 03:04 PM  说 :




谢谢 dunwan2tellu 的解。可是 x + y + z 未必是整数，而 AGM inequality 的条件是 n is integer.  ...

這個證明應該不需要x+y+z是整數
只要寫成指數形式就可以了

多普勒效应

小弟也提供一些不等式 =D
下列基本上都是讨论实数，括号里的是条件。
ms word 有问题，只好在 MathType 那边 print screeen 过来
字体不清，多多原谅 =P
（注: 第八题是 R+ ,不是 R-）
（第二题： d=max{a,b,c,d}）

dunwan2tellu

多普勒效应 于 5-7-2005 06:50 PM  说 :
小弟也提供一些不等式 =D
下列基本上都是讨论实数，括号里的是条件。
ms word 有问题，只好在 MathType 那边 print screeen 过来
字体不清，多多原谅 =P
（注: 第八题是 R+ ,不是 R-）
（第二题： ...

dunwan2tellu

８）
x^2 + y^2 +xy = 3/4 (x^2 + y^2 ) + 1/4 (x^2 + y^2 ) +xy

>= 3/4 (x^2 + y^2 ) +xy/2 + xy     

＝３／４ （x+y)^2

同理得另外两个 。 加起来就可以得证。

dunwan2tellu

怎么最近都没人来这里玩呢？那我就解第６题吧....

多普勒效应

pipi 老师最近较忙，
可能迟些再贴题..

dunwan2tellu

第５题真的被炸到！想来想去没想到将LHS-RHS就可以得到
(2b-c-d)(c-d)>=0 .....可惜，要不是有人提点，我还被陷在谷地呢...呵呵...