STPM 数学练习题

QooLuo

我是今年的中六生，数学很差。。
请各位帮我解答下面的数学题。。

1.Given that f(x) ≡ x^3 + kx^2 - 2x + 1 has a remainder k when it is divided by (x – k), find the possible value of k.
    已解

2.        Prove the following identities, for any sets A, B and C.
(a)        AU (B∩C) = (AUB) ∩ (AUC)
(b)        (A U B) ∩ (BUC) ∩ (CUA) = (A∩B) U (A∩C) U (B∩C)
(c)        A ∩ (B - C) = (A∩B) – (A∩C)
(d)        (A – C) ∩ (B –C) = (A∩B) – C
(e)        (A – B) U B = A if and only if  B is a proper subset of A
        已解


3.
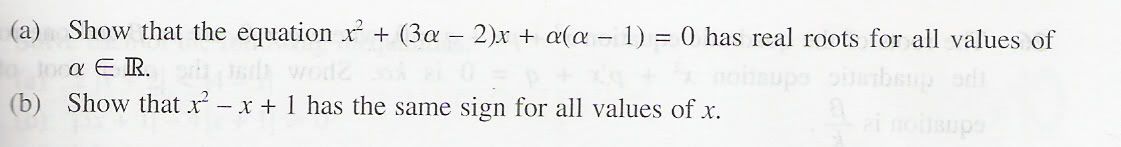
      已解

4.
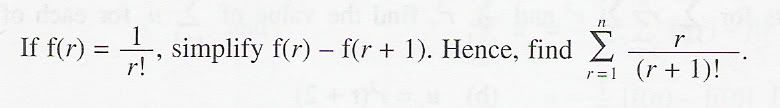
      已解
5.
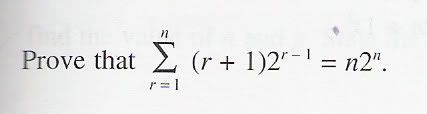
     已解

6.
     已解

7.        Two of the four sides of a parallelogram lie on the lines x - y + 1 = 0 and 2x + 3y - 6 = 0, and the two diagonals meet at the point ( 1, ½ ). Find the coordinates of the vertices of the parallelogram and the equation of the two remaining sides.
     已解

8.        Find the locus of the point P(x, y) such that the triangle with the point P(x, y) , A(5,0) and the origin, O, as vertices is right-angled at P.
       已解

9.      Find the set of values of x which satisfy the inequalities
        17 -  3x < 10/x

10.        Solve the inequality x^2 – 9 ≧(x + 3)(x^2 – 3x + 1)

[ 本帖最后由 QooLuo 于 5-9-2005 10:02 PM 编辑 ]

dunwan2tellu

1.Given that f(x) ≡ x3 + kx2 - 2x + 1 has a remainder k when it is divided by (x – k), find the possible value of k.

f(k)=k^3+k^3-2k+1=2k^3-2k+1 = k (remainder)

所以 2k^3 - 2k - (k-1) = 0 factorize 得

(k-1)(2k^2+2k+1)=0 .但 2k^2+2k+1=0无解，所以 k=1

dunwan2tellu

3a只需证明 b^2-4ac >0 即可。3b 则是b^2-4ac<0 后得x^2-x+1>0 即说明无论任何x，你都会有positive 的答案。

dunwan2tellu

第４题:

试试同分母就可以得到f(r)-f(r+1)= r/(r+1)!  .之后要找的sum其实就等于

[f(1)-(f2)]+[f(2)-f(3)]+...+[f(n)-f(n+1)] = f(1)-f(n+1)
=1- 1/(n+1)!

dunwan2tellu

５）

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 01:50 PM 发表


f(k)=k^3+k^3-2k+1=2k^3-2k+1 = k (remainder)

所以 2k^3 - 2k - (k-1) = 0 factorize 得

(k-1)(2k^2+2k+1)=0 .但 2k^2+2k+1=0无解，所以 k=1

为什么要用(k-1)呢？为什么不要用 x^3 + kx^2 - 2x +1除于 (x - k) 呢？

dunwan2tellu

因为remainder theorem 里说如果一个polynomial,f(x) divide by x-a 会有remainder ,R 的话，那么f(a) = R

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 01:55 PM 发表
3a只需证明 b^2-4ac >0 即可。

我不明白 3(a),我只做到
b^2 - 4ac = 5α^2 - 8α  +4

计算出来的答案不是 real number!

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 03:14 PM 发表
因为remainder theorem 里说如果一个polynomial,f(x) divide by x-a 会有remainder ,R 的话，那么f(a) = R

可是，为什么要是 2k^3 - 2k - (k-1) = 0，
而不是 2k^3 - 3k + 1 = 0 呢？

QooLuo

我看你还是写出算式，然后一边解释好了。。
因为我的理解能力很差。。
拜托了。。

dunwan2tellu

3a) 5a^2 - 8a +4 = 5(a-4/5)^2 + 4/5 > 0  用penyempurnaan kuasa dua 来做

dunwan2tellu

可是，为什么要是 2k^3 - 2k - (k-1) = 0，
而不是 2k^3 - 3k + 1 = 0 呢？

因为remainder theorem 告诉我们f(k)=k  (题目说明当x-k divide f(x) 时，remainder 是 k) .所以

f(k) = 2k^3 - 2k + 1 .

但是 f(k) = k ，所以 2k^3 - 2k + 1 ＝ k . 把k搬去左边得

2k^3 - 2k + 1 - k = 0 之后 再 factorize （之前做的）就可以了

dunwan2tellu

你也可以变成2k^3 - 3k + 1 =0 .之后你就必须用猜的方法才会知道k=1 。而我只不过是先将他factorize，因为当我搬k过来时看到可以factorize .

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 01:55 PM 发表
3b 则是b^2-4ac<0 后得x^2-x+1>0 即说明无论任何x，你都会有positive 的答案。

这个句子应该怎样写（in english)？？

dunwan2tellu

你只需要证明b^2-4ac<0 后注明 you will have positive sign for all value of x 即可

[ 本帖最后由 dunwan2tellu 于 13-8-2005 04:23 PM 编辑 ]

dunwan2tellu

8.        Find the locus of the point P(x, y) such that the triangle with the point P(x, y) , A(5,0) and the origin, O, as vertices is right-angled at P.

OP^2 + AP^2 = OA^2

(x^2+y^2) + {(x-5)^2+y^2} = 5^2  简化得

x^2 + y^2 -5x = 0

或 (x-5/2)^2 + y^2 = 25/4  既表示这locus是个圆形，center 在(5/2,0) ，半径是 5/2 .

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 01:59 PM 发表
第４题:

试试同分母就可以得到f(r)-f(r+1)= r/(r+1)!  .之后要找的sum其实就等于

[f(1)-(f2)]+[f(2)-f(3)]+...+[f(n)-f(n+1)] = f(1)-f(n+1)
=1- 1/(n+1)!

但， 我的老师教的不一样，他说

   r/ (r+1)! =[f(r) – f(r+1)]
             =  -  [f(r+1) – f&reg;]
             = -[f(n+1) – f(1)]
             = -{ [ (n+1)/((n+2)!) ] – (1/2) }
               :
               :
               :


他只教到这里，接下来的我不会做。。

dunwan2tellu

7.        Two of the four sides of a parallelogram lie on the lines x - y + 1 = 0 and 2x + 3y - 6 = 0, and the two diagonals meet at the point ( 1, &frac12; ). Find the coordinates of the vertices of the parallelogram and the equation of the two remaining sides.

因为是平行四方形，所以另两个line一定是 x - y + a=0 和 2x +3y +b =0 .

从 x - y + 1 = 0 和 2x + 3y - 6 = 0 解得intersecting point 是 （3/5 , 8/5) .又知道midpoint 是(1,1/2) ,所以 另一个vertex 必为 (1x2-3/5 , 1/2 x2 -8/5) = (7/5,-3/5) .但这point会pass through x - y + a=0 和2x +3y +b =0 。 所以带入便会得到 a=-2 , b=-1 .

既然４条line都找到了，自然，用２个line 来intersect 就可以得到另两个vertices

dunwan2tellu

但， 我的老师教的不一样，他说

   r/ (r+1)! =[f(r) – f(r+1)]
             =  -  [f(r+1) – f&reg;]
             = -[f(n+1) – f(1)]
             = -{ [ (n+1)/((n+2)!) ] – (1/2) }
               :
               :
               :


他只教到这里，接下来的我不会做。。

第３步有误！ -  [f(r+1) – f(r)] =\= -[f(n+1) – f(1)]

应该是 Sum {-  [f(r+1) – f(r)] } = -[f(n+1) – f(1)]
                              = -1/(n+1)! + 1

别忘了 f(r) = 1/r! 并不是 f(r)=r/(r+1)!

QooLuo

原帖由 dunwan2tellu 于 13-8-2005 04:41 PM 发表


OP^2 + AP^2 = OA^2

(x^2+y^2) + {(x-5)^2+y^2} = 5^2  简化得

x^2 + y^2 -5x = 0

或 (x-5/2)^2 + y^2 = 25/4  既表示这locus是个圆形，center 在(5/2,0) ，半径是 5/2 .

为什么 OP^2 + AP^2 = OA^2 ？