AMC的最後10題(高級卷)

灰羊

有些要圖的就暫時沒有...

21.
x + √( x^2 + √(x^3+1) ) =1有幾個實根?
a)0
b)1
c)2
d)3
e)4

23.展開(1-2x)^3(1+kx)^2,其中a和b是使得x^2係數為40的兩個k值,求a+b
a)-1
b)8
c)10
d)12
e)14

24.|x|+|y|=4的圖形所圍區域為多少?
a)2
b)4
c)8
d)16
e)32

25.2^2005的位數最接近(不能用計算機)
a)400
b)500
c)600
d)700
e)800

26至30題的答案自填0~999中的整數

27.對全體實數x,f(f(x))=6x-2005,若t滿足f(t)=6t-2005,求t

29.求1/x+1/y+1/z,已知x,y,z滿足
x+y+z=5
x^2+y^2+z^2=15
xy=z^2

30.一個正整數等於他的四個最小的正因子的平方和,求能整除此整數的最大質數

灰羊

原帖由 灰羊 于 4-8-2005 05:43 PM 发表
有些要圖的就暫時沒有...

21.
x + √( x^2 + √(x^3+1) ) =1有幾個實根?
a)0
b)1
c)2
d)3
e)4

23.展開(1-2x)^3(1+kx)^2,其中a和b是使得x^2係數為40的兩個k值,求a+b
a)-1
b)8
c)10
d)12
e)14

...

我的答案
21 b
23 d
24 e
25 d(錯了,應該是c)
27 401
29 5
30 不會做

hamilan911

第三十题是013。
那号码是130，最小公约数是1，2，5，10，平方和刚好是130。

hamilan911

我第21题被骗，所找到的根是0和2，但若把2带进，那等式不成立。

详圣

一個正整數等於他的四個最小的正因子的平方和,求能整除此整數的最大質數
这个题目中级也有啊。。。

多普勒效应

有一题是关于八面体的..
各位做到什么答案？

灰羊

原帖由 多普勒效应 于 4-8-2005 11:34 PM 发表
有一题是关于八面体的..
各位做到什么答案？

多普勒scan上來吧...
那題我一看到圖就不做了...
30題是用猜的啊???
21題不用算他的根出來,用韋塔定理就行了

灰羊

原帖由 多普勒效应 于 4-8-2005 11:34 PM 发表
有一题是关于八面体的..
各位做到什么答案？

你考到怎樣?
我有兩題5分題交了卷才想到...
這次應該100不到...

多普勒效应

考到还好啦..
题目校方收回去了..
今年用 A4 size 的，字大，个人满喜欢的 =P
听说成绩三个礼拜后就出了..
30 我也作不到

多普勒效应

AMC Senior 第28题..
英文版题目。请问谁有华文版的题目？



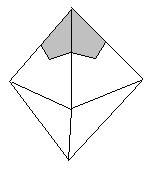
A regular octahedron has eight triangular faces and all sides the same length. A portion of a regular octahedron of volume 120cm^3 consists of that part of it which is closer to the top vertex then to any other one.In the diagram,the outside part of this volume is shown shaede,and it extends down to the centre of the octahedron. What is the volume,in cubic centimetres, of this unusually shaped portion.

多普勒效应

我Q28的答案是 020
我认为这个八面体是对称的，
所以, 整个八面体是由6个这样的"不规则型"
所以，我认为是 120/6 = 20

不过，我觉得我的解有错。
因为...
errrr....因为不太像"第二十八题"的解..^^"

dunwan2tellu

我回来了！

３０题是１３

我们知道最小的positive divisor 是１，所以１一定是四个positive divisor 之一。就设他们是

p = 1 + a^2 + b^2 + c^2

如果所有a,b,c都为奇，则RHS＝LHS＝偶 ，contradict .所以必有至少１个偶。就设a=2

p = 5 + b^2 + c^2

由于LHS＝偶 ，所以 b,c必须一奇一偶。就当b是奇，c是偶。而c只能是4 或2b .(不然c不会是smallest positive divisor之一）。

当c为４时，LHS＝０（mod 4)  , RHS = 1,2 (mod 4) 不可能。故c=2b .  我们有 p = 5 + 5b^2 ,而 不难看出p=0 (mod 5) 所一b只可以是5. c=2b=10

所以 1 + 2^2 + 5^2 + 10^2 = 130 是唯一的答案 ，而１３是最大的prime .

jinqwem

原帖由 多普勒效应 于 11-8-2005 01:07 AM 发表
我Q28的答案是 020
我认为这个八面体是对称的，
所以, 整个八面体是由6个这样的"不规则型"
所以，我认为是 120/6 = 20

不过，我觉得我的解有错。
因为...
errrr....因为不太像"第二十八 ...

很久的事，不过我也是那样解的。。。
我大概那时数学就没进步过，不进则退阿

dunwan2tellu

原帖由 jinqwem 于 12-3-2007 02:36 PM 发表

很久的事，不过我也是那样解的。。。
我大概那时数学就没进步过，不进则退阿

jinqwem , 怎么不断翻旧贴来讲啊？

jinqwem

原帖由 dunwan2tellu 于 12-3-2007 03:00 PM 发表


jinqwem , 怎么不断翻旧贴来讲啊？

弥补过去没参加佳丽的岁月啊