|
|
【纪念当年的帖子(2008)】高級數學纲要笔记
 [复制链接]
[复制链接]
|
|
|

楼主 |
发表于 2-1-2010 10:49 AM
|
显示全部楼层
Given that y=(5x+2)/(3x^3), find dy/dx
y=(5x+2)/(3x^3)
dy/dx =5(3x^3)-(5x+2)(9x^2)/(3x^3)^2
=(15X^3-45^3-18^2)/(3X^3)^2 --- (*)
=(-30X^3)/(3X^3) - (18X^2)/(3X^3)
=-10/3X^3 -2/X^4
你分母的 square 不见了..=.=
From (*), dy/dx = (-30x³-18x²)/(3x³)²
= (-30x³-18x²)/(9x⁶)
= 3(-10x³-6x²)/(9x⁶)
= (-10x³-6x²)/3x⁶
|
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 01:23 PM
|
显示全部楼层
发表于 2-1-2010 01:23 PM
|
显示全部楼层
我这题的做法对吗?
Given that f(x)=(18-4x)/3x^3,find dy/dx(2)
y=(18-4x)/3x^3
=[(-4)(3x^3) - (9x^2)(18-4x)]/3x^3
=(-12x^3 + 36x^3 - 162x^2)/(3x^3)^2
=(24x^3 - 162x^2)/9x^6
=3(8x^3 - 54x^2)/9x^6
=(8x^3 - 54x^2)/3x^6
=8/3x^3 - 18/x^4
=8/24 - 18/16
=-19/24
不懂对吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 01:52 PM
|
显示全部楼层
发表于 2-1-2010 01:52 PM
|
显示全部楼层
Given that g(x)=1/8(4x-3)^2 , evaluate g''(1/4)
g''是什么意思,请真人指点。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2010 01:57 PM
|
显示全部楼层
我这题的做法对吗?
Given that f(x)=(18-4x)/3x^3,find dy/dx(2)
y=(18-4x)/3x^3
dydx = [(-4)(3x^3) - (9x^2)(18-4x)]/3x^3
=(-12x^3 + 36x^3 - 162x^2)/(3x^3)^2
=(24x^3 - 162x^2)/9x^6
=3(8x^3 - 54x^2)/9x^6
=(8x^3 - 54x^2)/3x^6
=8/3x^3 - 18/x^4
=8/24 - 18/16
=-19/24
答案对了,但是为了省时间,红色的可以 skip,
直接 dy/dx (2) = ...
注:当你一开始 differentiate, y 就必须换成 dy/dx.. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2010 01:58 PM
|
显示全部楼层
Given that g(x)=1/8(4x-3)^2 , evaluate g''(1/4)
g''是什么意思,请真人指点。
Enceladus 发表于 2-1-2010 01:52 PM 
g'' 代表 differentiate 两次.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 01:59 PM
|
显示全部楼层
发表于 2-1-2010 01:59 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:05 PM
|
显示全部楼层
发表于 2-1-2010 02:05 PM
|
显示全部楼层
我知道了,可是g''是什么意思?
Enceladus 发表于 2-1-2010 01:59 PM 
g' 是differentiate一次
g"是differentiate 两次(再differentiate g') |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:06 PM
|
显示全部楼层
发表于 2-1-2010 02:06 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:10 PM
|
显示全部楼层
发表于 2-1-2010 02:10 PM
|
显示全部楼层
本帖最后由 walrein_lim88 于 2-1-2010 02:16 PM 编辑
做两次一样的东西,是吗?
Enceladus 发表于 2-1-2010 02:06 PM 
是
for example: g(x)=2(X^3)
g'(x)=6(X^2)
g"(x)=12X
Note: number of ' = how many times u differentiate (spm level until "/2times )
g"(x)= d2y/dx2
application:determine whether the point is max or min
g"<0, is negative,is max (我是酱来记,negative ,u very sad, is  <=mouth shape is n,so is max) <=mouth shape is n,so is max)
g">0,is positive,is min (u very happy, is  , mouth shape is u, is min) , mouth shape is u, is min) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:15 PM
|
显示全部楼层
发表于 2-1-2010 02:15 PM
|
显示全部楼层
Given that g(x)=1/8(4x-3)^2 , evaluate g''(1/4)
Enceladus 发表于 2-1-2010 01:52 PM 
y=1/8(4x-3)^2
dy/dx=8(-2)(4x-3)^-3(4)
=-64/(4x-3)^3
dy/dx'=-64(-3)(4x-3)^-4(4)
=768/(4x-3)^4
接下去我做到有点奇怪了,请前辈指点一下。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:26 PM
|
显示全部楼层
发表于 2-1-2010 02:26 PM
|
显示全部楼层
y=1/8(4x-3)^2
dy/dx=8(-2)(4x-3)^-3(4)
=-64/(4x-3)^3
dy/dx'=-64(-3)(4x-3)^-4(4)
...
Enceladus 发表于 2-1-2010 02:15 PM 
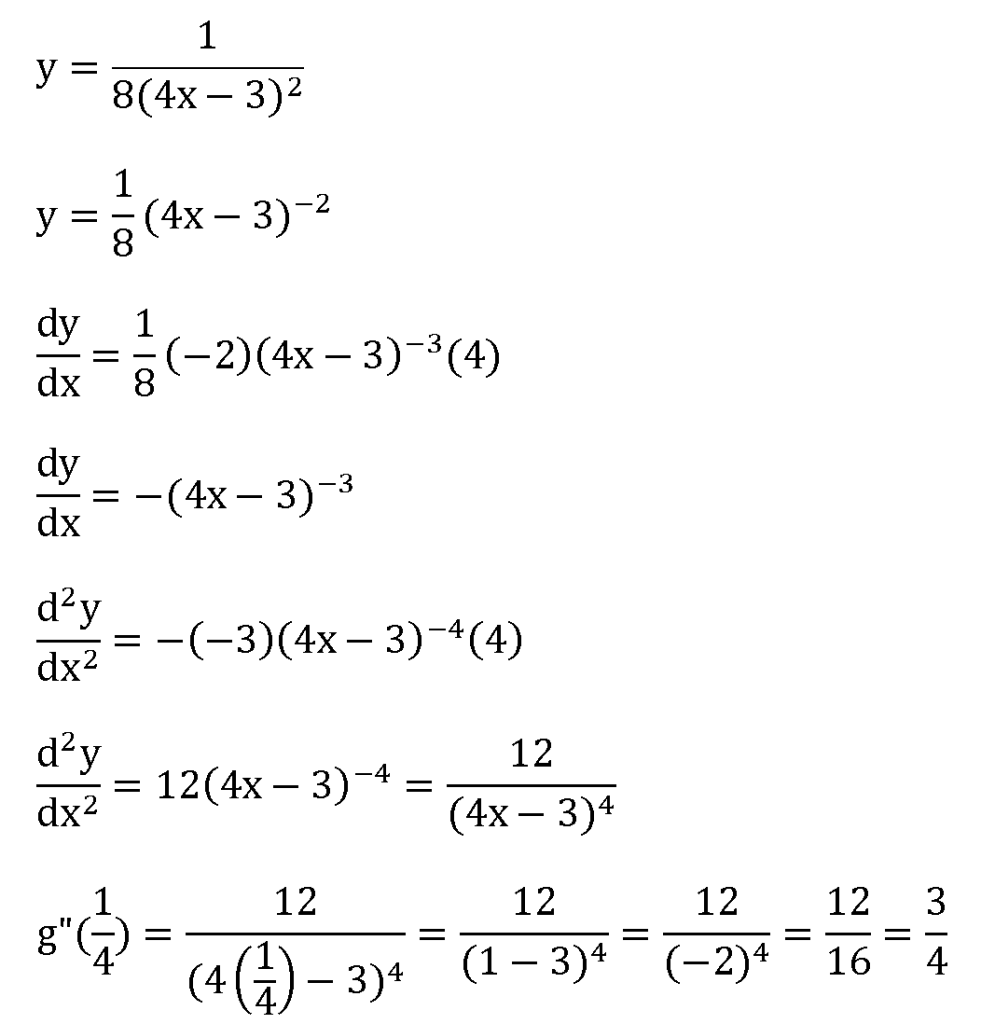
我觉得你g'(x)好像错了。所以g"会有点怪怪。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:30 PM
|
显示全部楼层
发表于 2-1-2010 02:30 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:31 PM
|
显示全部楼层
发表于 2-1-2010 02:31 PM
|
显示全部楼层
我又忘记掉真正的做法了,好彩有你提醒。
Enceladus 发表于 2-1-2010 02:30 PM 
你其实应该写1/8,不过你写成8,所以好像错了。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2010 02:34 PM
|
显示全部楼层
y=1/8(4x-3)^2
dy/dx=8(-2)(4x-3)^-3(4)
=-64/(4x-3)^3
dy/dx'=-64(-3)(4x-3)^-4(4)
...
Enceladus 发表于 2-1-2010 02:15 PM 
g(x) = 1/[8(4x-3)²] 不可以换成 8(4x-3)^-2,除非分母的前面没有 8.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:36 PM
|
显示全部楼层
发表于 2-1-2010 02:36 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:36 PM
|
显示全部楼层
发表于 2-1-2010 02:36 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2010 02:42 PM
|
显示全部楼层
回复 611# walrein_lim88
作答时,严重不可以把 g(x) 换成 y.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2010 02:45 PM
|
显示全部楼层
发表于 2-1-2010 02:45 PM
|
显示全部楼层
这个我知道,因为Enceladus写成y=....,做了最后才看到其实是g来的,所以我懒惰改回g了。。
y=1/8(4x-3)^2
dy/dx=8(-2)(4x-3)^-3(4)
=-64/(4x-3)^3
dy/dx'=-64(-3)(4x-3)^-4(4)
...
Enceladus 发表于 2-1-2010 02:15 PM  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-1-2010 06:18 PM
|
显示全部楼层
发表于 5-1-2010 06:18 PM
|
显示全部楼层
Given that y=(2x+1)(x-1)^3,find dy/dx.
dy/dx=2(x-1)^3 + 3(x-1)^2(2x+1)
=...........
接下去要怎样变,还有请解说为什么会这样子变? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 5-1-2010 06:28 PM
|
显示全部楼层
Given that y=(2x+1)(x-1)^3,find dy/dx.
dy/dx=2(x-1)^3 + 3(x-1)^2(2x+1)
=...........
接下去要怎样变?
Enceladus 发表于 5-1-2010 06:18 PM 
先排整齐,
dy/dx=2(x-1)^3 + 3(x-1)^2 .(2x+1)
在红色和蓝色里抽出公有(common)的东西,
i.e. dy/dx= (x-1)^2 [ 2(x-1) + 3(2x+1) ]
= (x-1)^2 (2x - 2 + 6x + 3)
= (x-1)^2 (8x + 1) |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|