数学训练（十月份）

灰羊

sinchee 于 9-10-2004 06:47 PM  说 :


不對﹗不對﹗﹗﹗
A先拿一部份,B把那堆拿剩一個,

還有情況4﹕
如果 A 將另一堆拿剩一個﹐
那麼﹐不管 B 怎麼拿﹐都輸了﹗﹗﹗﹗﹗
    : ...

謝謝指正,答案修正如下

A先拿,無論A拿哪一堆的多少個,B在另一堆也拿相同數量(2堆數量相等)
持續下去,因為A先拿,所以A一定先拿完其中一堆,B勝

你讓我的答案更精簡了

灰羊

sMIL3 于 9-10-2004 08:16 PM  说 :
为什么呢？图解不算解吗？

不是說不算解,只是用圖解每個人都行
應該是用泰勒展開式或其他方法來證明
這樣才夠嚴謹你認為呢???^^

pipi

sinchee 于 9-10-2004 06:47 PM  说 :
不對﹗不對﹗﹗﹗
A先拿一部份,B把那堆拿剩一個,

還有情況4﹕
如果 A 將另一堆拿剩一個﹐
那麼﹐不管 B 怎麼拿﹐都輸了﹗﹗﹗﹗﹗
    : ...

我也漏掉一些可能性。。。
paiser, paiser...

灰羊 于 10-10-2004 02:48 AM  说 :
謝謝指正,答案修正如下

A先拿,無論A拿哪一堆的多少個,B在另一堆也拿相同數量(2堆數量相等)
持續下去,因為A先拿,所以A一定先拿完其中一堆,B勝
你讓我的答案更精簡了

这与我的答案一样了。。。
（之前以为有不同的解法。。。也许还是有的！！）

pipi

sMIL3 于 9-10-2004 10:09 PM  说 :
首先，证明 ln(x/lnX)≥1:
y=ln(x/lnX)
dy/dx=(lnX-1)/(xlnX)
(e,1) is the minimum point lies on y

:.由此可知:
ln(π/lnπ)>1 (因为π>e)
lnπ-ln(lnπ)>1
lnπ>1+ln(lnπ)
lnπ>ln( ...

小心！！
我们先得设 x > 1, 那么才有 ln(x/lnX)≥1
接下来的做法没问题了！！

除了这方法，或许可试试类似
＂怎样画 x^y = y^x＂

[ Last edited by pipi on 22-10-2004 at 10:38 AM ]

灰羊

灰羊 于 4-10-2004 12:40 AM  说 :
以我的程度只能證一半

當π≦x≦2π
sin x≦0
(sin在第三第四象限為負值)

cos(cos x)≧0
(因為在第三第四象限-1≦cos x≦1
∴cos(cos x)≧0)

故當π≦x≦2π時,
cos(cos x)≧sin x
恆成立

以下是別人教我的 參考就好
我還沒學過微積分和泰勒級數

若0≦x≦兀,則利用泰勒級數展開法
設cosx=t ＝＞sinx= √(1-t^2),則原不等式變成cost≧√(1-t^2)
設cost的泰勒級數=f(t),√(1-t^2)的泰勒級數=g(t)
並令F(t)=f(t)-g(t)＝＞F’(t)=f’(t)-g’(t)
您將發現F’(t)≧0恆成立,此乃表示F(x)是遞增函數
∵-1≦t≦1,且F(-1)=0
∴cost≧√(1-t^2)
故cos(cosx)≧sinx
得證
(在此因數學符號不方便打,若您學過泰勒級數,請您自己試一下)

pipi 于 10-10-2004 08:16 AM  说 :

小心！！
我们先得设 x > 1, 那么才有 ln(x/lnX)≥1
接下来的做法没问题了！！

除了这方法，或许可试试类似
＂怎样画 x^y = y^x＂
[url]http://chinese.cari.com. ...

是的是的，没有想到。

eeCyang

11/10/2004，星期一
初中(A25) 若 a/b = b/c = c/d = d/a ，其中 abcd ≠0。
          求 (a+b+c+d)/(a+b+c-d) 之值。 （待解）
          （答案：）
          （解对者：）

a^2=c^2=bd, b^2=d^2=ac, ad=bc,ab=cd,

(a+b+c+d)/(a+b+c-d)
=1+2d/(a+b+c-d)

=1+2d(a+b+c+d)/[(a+b+c+d)*(a+b+c-d)]

=1+2(ad+bd+cd+d^2)/(a^2+b^2+c^2+2ab+2bc+2ac-d^2)

=1+2(ad+bd+cd+ac)/(2bd+2ab+2bc+2ac)   [a^2=c^2=bd, b^2=d^2=ac]

=1+2(ad+bd+cd+ac)/(2bd+2cd+2ad+2ac)   [ad=bc,ab=cd]

=1+1

=2

史奴比{^_^}

11/10/2004，星期一
初中(A25) 若 a/b = b/c = c/d = d/a ，其中 abcd ≠0。
          求 (a+b+c+d)/(a+b+c-d) 之值


a/b = d/a          b/c = c/d
a^2 = bd           c^2 = bd
a^2 = c^2 = bd
a = c = +/- (bd)^1/2

a/b = b/c          c/d = d/a
b^2 = ac           d^2 = ac
b^2 = d^2 = ac
b = d = +/- (ac)^1/2

(a+b+c+d)/(a+b+c-d) = (2a + 2b)/(2a)
                    =  1 + b/a
                    =  1 + b / [+/- (bd)^1/2]
                    =  1 + (b/d)^1/2  @ 1 - (b/d)^1/2
                    =  1 + 1   @  1 - 1
                    =  2  @  0      

pipi

02/10/2004，星期六
高中(B21) x 是任意实数，求证： cos(cos x) ≥ sin x 。

灰羊 于 10-10-2004 08:02 PM  说 :
以下是別人教我的 參考就好
我還沒學過微積分和泰勒級數

若0≦x≦兀,則利用泰勒級數展開法
設cosx=t ＝＞sinx= √(1-t^2),則原不等式變成cost≧√(1-t^2)
設cost的泰勒級數=f(t),√(1-t^2)的泰勒級數=g(t)
並令F(t)=f(t)-g(t)＝＞F’(t)=f’(t)-g’(t)
您將發現F’(t)≧0恆成立,此乃表示F(x)是遞增函數
∵-1≦t≦1,且F(-1)=0
∴cost≧√(1-t^2)
故cos(cosx)≧sinx
得證

这方法可行！！
现在试试用这个（比较快吧！！）

用Maclaurin Series,(可参考：这里)
cos(t) = 1 - 1/2(cos t)^2 + 1/24 (cos t)^4 - ... for ∞<t<∞.

所以
cos(cosx)≥ 1 - 1/2(cos x)^2    (因为|cos x|≤1)
         =  1/2 (2 - (cos x)^2)
         =  1/2 (1 + (sin x)^2)
         ≥ sin x

[ Last edited by pipi on 22-10-2004 at 10:41 AM ]

pipi

我又来呼吁大家尝试解一解那些" （待解） "的题目！！

03/10/2004，星期日
大专(C7)
        
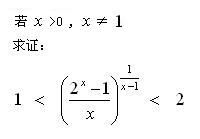
        （ 提示：利用 Mean Value Theorem ）   （待解）
        （答案：）
        （解对者：）

10/10/2004，星期日
大专(C8)
         （待解）
        （答案：）
        （解对者：）

史奴比{^_^}

12/10/2004，星期二
初中(A26) 已知 A,B,C,D,E 为整数，且 0 ≤A,B,C,D,E≤9 。

           若   A B C D E
             x          4
          _________________
                E D C B A  
               ----------
          求 A,B,C,D,E 之值。


4的乘法表 ：  0   1   2   3   4   5   6   7   8   9  
        -->   0   4   8   12  16  20  24  28  32  36

从A,E做起，

A x 4 = E (个位数)              E x 4 = *A
A = 1 or 2                 -->        = *1 or *2    (个位数是1或2)
(不可能是0,A不等于E)               E  =  - or 3/8     

If E=3, A=1
那么 A x 4 = E
     1 x 4 + (9) = 13  
-> 不可能 A=1, E=3,  1) 4 的乘法表最多能进位到3而已。
                     2) A x 4 只得单数。

所以可以确定，A=2, E=8

2***8 x 4 = 8***2


接下来找B, D,

B x 4 = D　(单数,没进位)    D x 4 + (3) = *B     (8x4 = 32, 进3)
B = 0 or 1 or 2                         = *0 or *1  or *2  
                                          (个位数是0或1或2)
                                     D  = -  or 2/7 or -

B 肯定是 = 1                        (D不可能是2 ， D不等于A)
                                    所以 D=7


最后找 C

D x 4 + (3) = 31  (进位3)


C x 4 + (3) = 3C    为何3C ? -->     B x 4 = D
                                     1 x 4 + (3) = 7   
                                    ( 需要从 C x 4 进位（3）)

所以结果 C 只能等于 9

答案：21978 x 4 = 87912  （若A B C D E 不重复）

如果A B C D E 重复， 那么答案是 00000 x 4 = 00000  

[ Last edited by 史奴比{^_^} on 12-10-2004 at 06:39 PM ]

灰羊

12/10/2004，星期二
初中(A26) 已知 A,B,C,D,E 为整数，且 0 ≤A,B,C,D,E≤9 。

           若   A B C D E
             x          4
          _________________
                E D C B A  
               ----------
          求 A,B,C,D,E 之值。
==========================================================

首先,A一定小於3,不然乘出來是六位數
∴A=2(因為E*4不會得到個位數1) => E=8

B也一定小於3,不然A*4不會得E,
考慮B≠2,因為上面E*4後會進位3,所以B一定是奇數
∴B=1 => D=7 (因為D*4後加上進位的3得到個位數1,且D＞4)

D=7,所以上面D*4後加上進位的3=31,進位3,
0≤C≤9,且C*4加上進位的3後.會進位3
∴C=9

(A,B,C,D,E)=(2,1,9,7,8)

灰羊

13/10/2004，星期三
初中(A27) 甲、乙兩人轮流报数，必须报不大於2的自然数，把兩人报的数加起來，
          谁报数后加起來的数是20，谁就获胜。
          如甲要取胜，是先报还是后报？报几？（请解释你的论点！）
=========================================================================

甲先報!報2,接下來對方報2甲就報1,對方報1甲就報2,甲必勝!

因為報的數必須是1或2,所以每一次
甲跟乙報的數的和一定可以湊成3
3*6=18,甲如果先報2,解下來把自己報的數
和乙報的數湊成3,哪麼甲第7次報數就能湊成3*6+2=20
就能勝利了!!!!!^^Y

灰羊

為甚麼這裡的人只來數學訓練???
我發了2篇問題
一個解幾 一個數論
都沒有人理我....回覆0....

14/10
半径平方的4倍

情~風

10/10/2004 星期日
大专(C8)

(a)
n + Sn
= n + 1 + 1/2 + ... + 1/n
= 2 + 3/2 + 4/3 + 5/4 + ... + (n+1)/n
>= n{(2)(3/2)(4/3)...[(n+1)/n]}^(1/n) by AM-GM inequality
= n(n+1)^(1/n)
Since 2 =/= 3/2 =/= ... =/= (n+1)/n, so the equality won’t hold.
Thus n + Sn > n(n+1)^(1/n).

Method for (b) is similar to that of (a).
n - Sn
= n - 1 - 1/2 - ... - 1/n
= 1/2 + 2/3 + 3/4 + ... + (n-1)/n
>= (n-1){(1/2)(2/3)(3/4)...[(n-1)/n]}^[1/(n-1)] by AM-GM inequality
= (n-1)(1/n)^[1/(n-1)]
= (n-1)n^[-1/(n-1)].
Since 1/2 =/= 2/3 =/= ... =/= (n-1)/n, so the equality wont hold.
So n - Sn > (n-1)n^[-1/(n-1)].

fritlizt

13/10/2004，星期三
初中(A27) 甲、乙兩人轮流报数，必须报不大於2的自然数，把兩人报的数加起來，
          谁报数后加起來的数是20，谁就获胜。
          如甲要取胜，是先报还是后报？报几？（请解释你的论点！） （待解）
          （答案：）
          （解对者：）

答案：先报数的赢。报 2 号。


如果先报到 20 号的赢。也就是说报17号的赢了。
如此推算，报2号的赢定。

[ Last edited by fritlizt on 15-10-2004 at 12:57 AM ]

38女

12/10/2004，星期二
初中(A26) 已知 A,B,C,D,E 为整数，且 0 ≤A,B,C,D,E≤9 。

           若   A B C D E
             x          4
          _________________
                E D C B A  
               ----------
          求 A,B,C,D,E 之值。 （待解）
          （答案：）
          （解对者：）

由题目,知道A<E,而且A*4一定会是个位数,因此A只能是1或2.A若是1的话,E就是4了,而E*4不等于A=1.
因此,A=2;E=8.
接着B*4也一定是个位数,也知道B<D.由于A=2;E=8,那E*4=8*4=32,进位3.
D*4+3的个位数要小于D.因此D只能是7,7*4+3=31,所以B=1,进位3.
然后,C*4+3的个位数要是C,因此只有C=9,因为9*4+3=39.C=9,进位3.

最终的答案便是:
    21978
  x     4
---------
    87912
---------

38女

13/10/2004，星期三
初中(A27) 甲、乙兩人轮流报数，必须报不大於2的自然数，把兩人报的数加起來，
          谁报数后加起來的数是20，谁就获胜。
          如甲要取胜，是先报还是后报？报几？（请解释你的论点！） （待解）
          （答案：）
          （解对者：）

先报,而且要报到2,然后报(2+3),再报(2+3+3),(2+3+3+3)...

曾经和家人玩过的游戏.其实决定关键在于心算要快.
比如:最终数为50,一次可报不大于3的自然数,那就以50-(3+1)-(3+1)-(3+1)...,减至最后,你会获得2.那你只要先报2,然后循序报6,10,14,18,22...一直加4,就可以先报到50了.

38女

14/10/2004，星期四
高中(B25) 如图，在圆 O 任意画二 互相垂直的(chord)：AB 及 CD。
          若 AB 与 CD 交点为 P 。
          求证： AP^2 + PB^2 + CP^2 + PD^2 恒为某定值。
           （待解）
          （答案：）
          （解对者：）
我不是很明白"恒为某定数"的意思...然而,我还是尝试了,希望我没误解.

解:
设CAP的角为Y,DBP的角为X.
AP = AC cosY
PB = DB cosX
CP = AC sinY
PD = DB sinX

因此,
AP^2 + PB^2 + CP^2 + PD^2
= (AC cosY)^2 + (DB cosX)^2 + (AC sinY)^2 + (DB sinX)^2
= AC^2 ((cosY)^2 + (sinY)^2) + DB^2 ((cosX)^2 + (sinX)^2)
= AC^2 + DB^2

对吗?