STPM-学校功课討論区

hamilan911

z1+z2 = (a+b+(2a+b)i)/(-1+3i) = 1
a+b=-1
2a+b=3
a=4, b =-5

darksider

原帖由 hamilan911 于 2008/5/25 03:17 PM 发表
z1+z2 = (a+b+(2a+b)i)/(-1+3i) = 1
a+b=-1
2a+b=3
a=4, b =-5

谢谢！

现在又有个问题解不了。

The complex number z is given by z = 1 + cos dita + i sin dita
where -pie < dita 《 pie

a)find the modulus and argument of z and 1/z when dita = pie / 3

我找到答案，但都是通过prematured approximation的，给的答案的imaginary part是有surd的，找不到 :x

flash

原帖由 darksider 于 25-5-2008 05:13 PM 发表


谢谢！

现在又有个问题解不了。

The complex number z is given by z = 1 + cos dita + i sin dita
where -pie < dita 《 pie

a)find the modulus and argument of z and 1/z when dita = pie / 3

...

你问的是 z 还是 1/z 的 imaginary part? 不过不管怎样，当 dita = pie/3 这两个的 imaginary part 的确有 surd, 看回一些 common angles 的值你就会懂了。。。。。。

darksider

原帖由 flash 于 2008/5/25 07:28 PM 发表



你问的是 z 还是 1/z 的 imaginary part? 不过不管怎样，当 dita = pie/3 这两个的 imaginary part 的确有 surd, 看回一些 common angles 的值你就会懂了。。。。。。

我问both z 和

hamilan911

z= 1+cospi/3 +i sinpi/3 = 3/2 + isqrt3/2
modulus z = sqrt3
argument z = arc tan 1/sqrt3 = pi/6


1/z = (1+cosA-isinA)/(1+cosA +isinA)(1+cosA-isinA)
      = (1+cosA-isinA)/(2+2cosA)
      = (2cos^2[A/2] - i2sin[A/2]cos[A/2])/(4cos^2[A/2])
      = 1/2  - i1/2tan[A/2]
A = pi/3
1/z = 1/2 - i 1/(2sqrt3)

modulus 1/z = 1/sqrt3
argument 1/z = arc tan (-1/sqrt3) = - pi/6


如flash兄说的，要懂common angles

darksider

大家好，这些问题都是我目前solve不到的。
20）Find the constant a such that for all real values of b, one of the roots of the equation 2x^3 + ax + 4 = b(x-2) is .
       （i）When a takes this value, find the set of values of b where the given equation has three real and distinct roots.
         

35) if (3 - i )^(1/2)
         --------------  = x + yi , where x and y are real numbers , find the value of x and y.
           1 + i

37) if (x + iy )^2 = x + iy , where x and y are real numbers, find the possible values of x and y.

38) Determine value of a if 3^(1/2) + ai  is a real number, and find this number.
                                          --------------  
                                           1- 3^(1/2)i

谢谢！

darksider

原帖由 hamilan911 于 2008/5/25 09:22 PM 发表
z= 1+cospi/3 +i sinpi/3 = 3/2 + isqrt3/2
modulus z = sqrt3
argument z = arc tan 1/sqrt3 = pi/6


1/z = (1+cosA-isinA)/(1+cosA +isinA)(1+cosA-isinA)
      = (1+cosA-isinA)/(2+2cosA)
      = (2co ...

谢谢，现在在思考着。



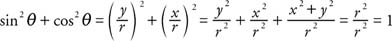
为何 y^2 + x^2 + x^2 + y^2 = r^2? (numerator)?

[ 本帖最后由 darksider 于 25-5-2008 11:14 PM 编辑 ]

hamilan911

原帖由 darksider 于 25-5-2008 10:00 PM 发表


谢谢，现在在思考着。



为何 y^2 + x^2 + x^2 + y^2 = r^2? (numerator)?

是等号来的

flash

原帖由 darksider 于 25-5-2008 10:00 PM 发表


谢谢，现在在思考着。



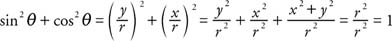
为何 y^2 + x^2 + x^2 + y^2 = r^2? (numerator)?

那个加号应该是等于号吧。。。。。。。

(x/r)^2 + (y/r)^2 = y^2/r^2 + x^2/y^2 = (x^2+y^2)/r^2 = r^2/r^2 = 1
因为 r = (x + y)^1/2 。。。。。。。

hamilan911

35. (3-i)^1/2 = (x+yi)(1+i) = x-y +(x+y)i
square both side,
3-i = x^2+y^2-2xy - (x^2+y^2+2xy) + 2(x^2-y^2)i
3 = -4xy
-1 = 2(x^2 - y^2)
... solve x and y

37. (x+yi)^2 = x+yi
(x+yi)(x+yi -1) = 0
x+yi = 0   -> x,y =0
x+yi-1 =0 -> x=1, y =0

另一个做法
(x+yi)^2 = x^2 - y^2 +2xyi = x+yi
2xy = y       -(1)   
x^2-y^2= x   -(2)
from (1), y(2x-1) = 0  -> y=0, x = 1/2

when x = 1/2, subs into (2)
1/4 - y^2 = 1/2  -> y^2 = -1/4  -> y = 1/2i (imaginary, rejected)

so y=0, x^2 = x , x(x-1)=0 , x=0, 1
(x,y) = (0,0), (1,0)

39. (sqrt3+ai)(1+sqrt3i)/(1-sqrt3i)(1+sqrt3i) = [(1-a)sqrt3 +(3+a)i]/ 4
if it is a real number, 3+a =0, so a=-3

第20题题目不清楚，if one of the roots of the equation ... is ??,那个root是什么？？
可以尝试自己做

darksider

原帖由 hamilan911 于 2008/5/25 11:56 PM 发表
35. (3-i)^1/2 = (x+yi)(1+i) = x-y +(x+y)i
square both side,
3-i = x^2+y^2-2xy - (x^2+y^2+2xy) + 2(x^2-y^2)i
3 = -4xy
-1 = 2(x^2 - y^2)
... solve x and y

37. (x+yi)^2 = x+yi
(x+yi)(x+yi -1) = ...

谢谢，明天早上才做了。

第20, one of the root of the equation 2x^3 + ax + 4 = b(x-2) is 2，

i)When a takes this value, find the set of values of b where the given equation has three real and distinct roots.
我找到答案了，b〉－４，但不懂为何　ｂdoes not equal 14.(答案里写的）

ii)When a =-10 , b = -12 , find the real and complex roots of the above equation.
                         (这题都没有imaginary part,怎能找到complex root阿?)

[ 本帖最后由 darksider 于 26-5-2008 01:21 PM 编辑 ]

darksider

原帖由 flash 于 2008/5/25 11:41 PM 发表




那个加号应该是等于号吧。。。。。。。

(x/r)^2 + (y/r)^2 = y^2/r^2 + x^2/y^2 = (x^2+y^2)/r^2 = r^2/r^2 = 1
因为 r = (x + y)^1/2 。。。。。。。

知道了，谢谢！

darksider

原帖由 hamilan911 于 2008/5/25 09:22 PM 发表
z= 1+cospi/3 +i sinpi/3 = 3/2 + isqrt3/2
modulus z = sqrt3
argument z = arc tan 1/sqrt3 = pi/6


1/z = (1+cosA-isinA)/(1+cosA +isinA)(1+cosA-isinA)
      = (1+cosA-isinA)/(2+2cosA)
      = (2co ...

这题是Q20的（ii），第（i）的已经会做了。
ii) Show that for all values of dita, the point representing z in a argand diagram is located on a circle. Find the centre and radius of the circle.

这题的是（iii），我做了，以下是我的解法，不知能不能这样做。

iii)Prove that the real part of 1/z is 1/2 for all values of dita.

        Let dita = any angels.

1/z = 1+ cos dita            sin dita i
       -------------------   -  ----------------
         2+ 2 cos dita         2+ 2 cos dita

since all real part = 1/2 , when comparing ,
       1 + cos dita
        ---------------      = 1/2
        2+ 2 cos dita

Let cos dita = m

LHS = 1 + m
          ----------
            2+ 2m

LHS = 1(1+m)
            -----------
            2(1+m)

LHS = 1                           LHS = RHS
           ---                               (proven)         
            2              

这样的做法能被接受吗？

hamilan911

b does not equal 14,因为你要注意它有three distinct roots，所以你要set root formula [ (-b+-sqrt{b^2-4ac)/2a ] =/= 2,你就会找到b不等于14

(ii)不难，你只要express整个equation成(x-2)P(x)，再从P(x)那边把root找出来，roots = 2, -1+2i, -1-2i


楼上这题，你酱证明是错的，做法很“怪”，你不可以先set RHS = 1/2

你应该写
real part = (1+cosA)/(2+2cosA) = (1+cosA)/2(1+cosA) = 1/2 就行了

darksider

原帖由 hamilan911 于 2008/5/26 02:13 PM 发表
b does not equal 14,因为你要注意它有three distinct roots，所以你要set root formula [ (-b+-sqrt{b^2-4ac)/2a ] =/= 2,你就会找到b不等于14

(ii)不难，你只要express整个equation成(x-2)P(x)，再从P(x)那边把 ...

真的谢谢，原来那些都是多余的，头脑不灵活

至于第二的，我一直以为去quadratic equation 不会有imaginary的root，刚刚做了，原来是有的，谢谢！

b does not equal 14,我没有用set root formula，我用b^2 - 4ac > 0 , 应该没有exception了吧？

[ 本帖最后由 darksider 于 26-5-2008 06:02 PM 编辑 ]

harry_lim

這里的人真的是很厲害中六的maths
我嚇到了

hamilan911

如果你用b^2 - 4ac>0, 你就只找到b>-4

我的意思是除了用b^2-4ac>0找出b>-4，你还要用root不等于2的原理
所以 (-4+sqrt[32+8b]) / 4  =/=  2
32+8b =/= 144
b =/= 14

这就是你要问的“不懂为何b does not equal 14"

darksider

原帖由 hamilan911 于 2008/5/26 09:38 PM 发表
如果你用b^2 - 4ac>0, 你就只找到b>-4

我的意思是除了用b^2-4ac>0找出b>-4，你还要用root不等于2的原理
所以 (-4+sqrt[32+8b]) / 4  =/=  2
32+8b =/= 144
b =/= 14

这就是你要问的“不懂为何b does not eq ...

现在懂了，谢谢指点！

为何要用root不等于2的原理？
因为这个equation的roots是distinct的，所以找到了root 2后，其余的root不可能会是2。

对吧？

[ 本帖最后由 darksider 于 26-5-2008 10:35 PM 编辑 ]

hamilan911

对了，就是酱

darksider

原帖由 hamilan911 于 2008/5/27 10:00 AM 发表
对了，就是酱

这题是Q18 的 ii
The complex number z is given by z = 1 + cos dita + i sin dita
where -pie < dita 《 pie

ii) Show that for all values of dita, the point representing z in a argand diagram is located on a circle. Find the centre and radius of the circle.

虽然我知道，不管 theta是什么value，z一定会在 unit circle里面，而且那个radius是1（hypotenuse),但要怎样回答？