多普勒的趣题分享 (11/11 新加题目)

mathlim

两位版主都很优秀，
在这里获益不浅。

jhwong_alen

原帖由 多普勒效应 于 2-9-2007 09:38 PM 发表
好的, 再来一题



这两题都是近年来的澳洲数学比赛赛题!

答案是36个边的正多边形？？

多普勒效应

原帖由 jhwong_alen 于 3-9-2007 01:41 PM 发表


答案是36个边的正多边形？？

不是 36是 n 的可能值之一, 不过不是最小的.
不妨贴解答上来大家看看

[ 本帖最后由 多普勒效应 于 3-9-2007 03:21 PM 编辑 ]

mathlim

很多的数学论坛，就是题目跟答案！
我们要的是网上学习。
不但要有做法，最好还有解题思想等。
有时候知道为什么错比知道对更重要。
知道正确的做法，而不知道为什么错，
那么同样的错误就很容易会重犯。

jinqwem

第三题答案是不是二十?

flash

原帖由 jinqwem 于 3-9-2007 08:58 PM 发表
第三题答案是不是二十?

我好像是算到 36，不知道对吗。。。。。

mathlim

我也把我的做法一般化：

P1—1/1—P2—1/2—P3—1/3—P4—……—Pn-2—1/(n-2)—Pn-1—1/(n-1)—Pn

红色的分数表示两个点之间的距离。
以下为每一段距离所需计算的次数。

1/1 : 1×(n-1)
1/2 : 2×(n-2)
1/3 : 3×(n-3)
...
...
1/(n-2) : (n-2)×2
1/(n-1) : (n-1)×1

这些点中所有两个点之间的距离的总和为
1×(n-1)×1/1 + 2×(n-2)×1/2 + 3×(n-3)×1/3 + … … + (n-2)×2×1/(n-2) + (n-1)×1×1/(n-1)
= (n-1) + (n-2) + (n-3) + … … + 2 + 1
= n(n-1)/ 2

jinqwem

原帖由 flash 于 4-9-2007 01:30 PM 发表


我好像是算到 36，不知道对吗。。。。。

不好意思, 之前算太快了...
同意是36...

多普勒效应

第三题答案是36
大家可以大概的解释一下你们的做法吗?

flash

是考虑到能把那个字分成几节， 如 MATHEMATICS 是 1 节, MATHE-MATICS 是 2 节, MA-THE-MATICS 是 3 节; 然后把每节的可能性加起来。

dunwan2tellu

Generalise Q3 :

v_i = i th vowel ,  a_i = consonant bewteen 2 consecutive vowel v_i and v_(i+1)

If number of vowel = n , then

Total Permutation = (a_1 + 2)(a_2 + 2)(a_3 + 2)...(a_(n-1) + 2)

Example : MATHEMATIC

v_1 = A , v_2 = E , v_3 = A , v_4 = I

a_1 = 2 , a_2 = 1 , a_3 = 1

Total permutation = (2+1)(1+2)(1+2) = 36

dunwan2tellu

Generalise Q2:

If the angle of intersection between 2 diagonals of a n-regular polygon = t

min{ n } = 180/[gcd(180,t)]

jinqwem

原帖由 dunwan2tellu 于 4-9-2007 09:31 PM 发表
Generalise Q3 :

v_i = i th vowel ,  a_i = consonant bewteen 2 consecutive vowel v_i and v_(i+1)

If number of vowel = n , then

Total Permutation = (a_1 + 2)(a_2 + 2)(a_3 + 2)...(a_(n-1) + ...

版主打错了,
应该是( 2+2)(2+1)(2+1)

mathlim

有一个正多边形，它有两条对角线的交角为50°。请问这个正多边形至少要有几个边才有此可能？


我真的很怕看到题目，因为常常欲罢不能！
结果把其他事情都耽误了。
今天才尝试解这一道题，
没想到立刻有灵感。
这的确是个有趣的题目。
我把解答贴上来分享。

mathlim

把正n边形的n个顶点均匀的分布在圆心为原点，半径为1的圆上。
设：
P1(cos(2π/n), sin(2π/n)),
P2(cos(4π/n), sin(4π/n)),
P3(cos(6π/n), sin(6π/n)),
…
…
Pn-1(cos(2(n-1)π/n), sin(2(n-1)π/n)),
Pn(cos2π, sin2π) = Pn(1, 0)。
设圆上任意两点：
Ps(cos(2sπ/n), sin(2sπ/n)),
Pt(cos(2tπ/n), sin(2tπ/n))。
m1 = mPsPn = sin(2sπ/n) / [ cos(2sπ/n) – 1 ],
m2 = mPtPn = sin(2tπ/n) / [ cos(2tπ/n) – 1 ]。
50°= 5π/18
tan(5π/18) = | (m1 – m2) / (1 + m1m2) | (略)
= | tan[(s-t)π/n] |
∴ n 的最小正整数值为18。
答：这个正多边形至少要有十八个边才有此可能。

[ 本帖最后由 mathlim 于 4-9-2007 10:43 PM 编辑 ]

多普勒效应

mathlim兄和dunwan2tellu兄都很厉害!

想不到那题可以用解析几何解！
mathlim的解答中有一个公式:

多普勒效应

这个是我第二题的解答，和mathlim兄的解答比较不一样：

多普勒效应

再来一题 ^^

mathlim

原帖由 多普勒效应 于 5-9-2007 12:06 AM 发表

我想提出一个疑问，若边数为奇数，对角线不经过中心，上述结果似乎不成立！

mathlim

原帖由 多普勒效应 于 5-9-2007 12:04 AM 发表

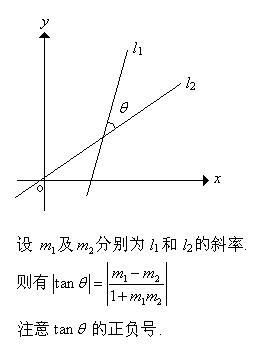
如果m1至m2是顺时针方向的话，绝对值符号可省！
tanθ = (m1 - m2)/(1 + m1m2)

夹角公式之所以要有绝对值符号，
是因为我们定义两条不平行的直线的夹角为锐角。
如果我们要求两条直线的某个交角(也可以是钝角)，
那么就要依顺时针方向，
两条直线的斜率相减。