数学比赛常出题目

dunwan2tellu

原帖由 shingrons 于 11-11-2006 10:24 AM 发表


请教dunwan2tellu
要深入研究是不是关系到mod模？
我才高二罢了....明年好像才上...

本来我是要用 mod 来解释，不过怕可能没学过，所以就用这个和 mod 相同的概念解释。

lavendar_o5

可以教教我如何用Mod做嗎？　

lavendar_o5

數學比賽常出的題目，數目通常都很大。有高手可以在這裏分享分享一些數學“技巧”嗎？如：

1）請問 1 x 2 x 3 x 4 x 5 x ... x 100 有多少個0在後面 ？
答:
設 [x] 爲小於x的最大整數

[100 / 5] + [ 100 / 25 ] = 20 + 4 = 24
所以共有24個0在後面。

2) 請問36有多少個Factor ? (當然題目不會問這麽小的數字）
答:
36 = 2 ^ 2 * 3 ^ 2
(2 + 1) * (2 + 1) = 9
所以36有9個Factor.

3）將0.812348123481234...寫成分數。
答：

0.812348123481234 = 81234 / 99999 (分子與分母的digit一樣多，唯分母一定由9組成）

望數學高手們可以分享，讓我這個井底之蛙可以見識見識。

[ 本帖最后由 lavendar_o5 于 13-11-2006 11:48 PM 编辑 ]

dunwan2tellu

原帖由 lavendar_o5 于 13-11-2006 11:35 PM 发表
可以教教我如何用Mod做嗎？　

试试 google search " modular arithmetic " 吧！

lavendar_o5

原帖由 dunwan2tellu 于 13-11-2006 11:45 PM 发表


试试 google search " modular arithmetic " 吧！

現馬上找，謝謝您。

lavendar_o5

原帖由 shingrons 于 11-11-2006 10:24 AM 发表


请教dunwan2tellu
要深入研究是不是关系到mod模？
我才高二罢了....明年好像才上...

在网上搜查了一下，刚学会Mod，现贴上我的做法，如果发现做法太长或演算有问题，望大家指教:





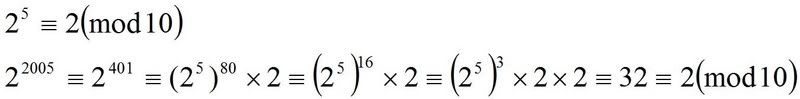
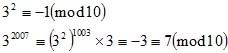
总结: 2 ^ 2005，Last Digit = 2; 3 ^ 2007, Last Digit = 7

[ 本帖最后由 lavendar_o5 于 16-11-2006 01:47 AM 编辑 ]

dunwan2tellu

原帖由 lavendar_o5 于 16-11-2006 01:45 AM 发表


在网上搜查了一下，刚学会Mod，现贴上我的做法，如果发现做法太长或演算有问题，望大家指教:



http://i105.photobucket.com/albums/m233/ ...

基本上就如你所做。如果要找 last two digit 就等于找 mod 100 , 找 last three digit 等于找 mod 1000 ... 以此类推。当然，要找的模(mod) 越大，就越困难。

kbubble

那 2^100 有多少位数是不是和你们所讨论的题目有异曲同工之处?

flash

原帖由 kbubble 于 17-6-2007 11:33 AM 发表
那 2^100 有多少位数是不是和你们所讨论的题目有异曲同工之处?

这个可以用 log 来做。。。。。
roundup(100 *log 2) ＝ 31
所以共有 31 位数

kbubble

100 *log 2 可以相等于 2^100吗?

flash

原帖由 kbubble 于 17-6-2007 07:08 PM 发表
100 *log 2 可以相等于 2^100吗?

100 * log 2 当然不等于 2^100。。。。问题你的题目是要找有关号码有多少位数，所以就用这个方法。

Leong13

樓上的，我是新手，可以explain為什麼要這樣做嗎？

flash

原帖由 Leong13 于 18-6-2007 08:22 PM 发表
樓上的，我是新手，可以explain為什麼要這樣做嗎？

假设 2^100 = X = A * 10^B； 1<=｜A｜ < 10
那 X 就有 B+1 个位数，所以要找有关号码有多少位数就

roundup(log (2^100)) = roundup(log(A)+ B) = B + 1