|
|
 发表于 30-11-2005 01:25 AM
|
显示全部楼层
发表于 30-11-2005 01:25 AM
|
显示全部楼层
原帖由 dunwan2tellu 于 28-11-2005 07:49 PM 发表
那么有何方法可以先证明S是收敛的呢?
用La' Hopital's Rules应该就可以证明了,那么就可以用infinite series来解,就没有破绽了。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-11-2005 10:02 AM
|
显示全部楼层
发表于 30-11-2005 10:02 AM
|
显示全部楼层
原帖由 hamilan911 于 29-11-2005 03:44 PM 发表
= 1 + 1/2S + 1/3S - 1/6S
酱解释会较清楚吧,其实这就是用到那个set的P(AUB) = P(A) + P(B) - P(A N B) [\color] ...
做法是很创意,可是忽略了利用的概念的细节. 你用的公式里每一项都有上界, 而运用于无穷级数,除非先证明那无穷级数有上界(收敛),要不这个证明还有漏洞。请别误会这是鸡蛋里挑骨头,只是想指出其中的不足。
至于要证明 S 是收敛的就必须再想了,或许不容易。
[ 本帖最后由 铁蛋 于 30-11-2005 10:03 AM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-11-2005 03:28 PM
|
显示全部楼层
|
whitelighter , 请问如何用 L' Hopital Rules 来证明啊 ? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 31-12-2005 08:11 PM
|
显示全部楼层
来试试看这题级数,当做是迎接2006年 
1!(1^2+1+1) + 2!(2^2+2+1) + 3!(3^2+3+1)+...+2006!(2006^2+2006+1) = ?
注:Pattern 是 k!(k^2 + k + 1) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2006 04:30 AM
|
显示全部楼层
发表于 2-1-2006 04:30 AM
|
显示全部楼层
(K+2)! = (K+2).(K+1)!
= K.(K+1)! + 2(K+1)!
= K.(K+1).K! + + 2(K+1)!
= (K^2 + K).K! + K! - K! + 2(K+1)!
= (K^2 + K + 1).K! - K! + 2(K+1)!
SO:
(K^2 + K + 1).K! = (K+2)! + K! - 2.(K+1)!
K = 1 TO 2006;
SUM[(K^2 + K + 1).K!] = SUM[(K+2)! + K! - 2.(K+1)!]
= 3! + 1! - 2 x 2! k = 1
+ 4! + 2! - 2 x 3! k = 2
+ 5! + 3! - 2 x 4! k = 3
.
.
.
.
.
+ 2008! + 2006! - 2 x 2007! k = 2006
= 1! - 2! + 2008! - 2007! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2006 01:40 PM
|
显示全部楼层
你也可以继续简化得到
(k+2)!+k!-2(k+1)! = [(k+2)!-(k+1)!] - [(k+1)!-k!]
=(k+1)(k+1)! - k.k!
所以sum = 2007.2007! - 1
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 2-1-2006 03:38 PM
|
显示全部楼层
发表于 2-1-2006 03:38 PM
|
显示全部楼层
SUM[(K^2 + K + 1).K!] = 1! - 2! + 2008! - 2007!
= 1 - 2 + 2008x2007!-2007!
= 2007 x 2007! - 1
[(K+2)! + K! - 2.(K+1)!] = [(K+2)! - (K+1)! ] - [(K+1)! -k!]
我怎么没想到!!!哈哈。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 2-1-2006 04:52 PM
|
显示全部楼层
好吧,来一题较有挑战性的!
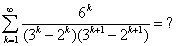 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-1-2006 04:03 PM
|
显示全部楼层
发表于 4-1-2006 04:03 PM
|
显示全部楼层
E(k=1, infinity)6^k / (3^k - 2^k)(3^(k+1) - 2^(k+1))
= E(k=1, infinity) [3^k / (3^k - 2^k)] - [3^(k+1)/ (3^(k+1) - 2^(k+1))]
= 3/(3-2) - 9/(9-4) + 9/(9-4) - 27/(27-8) +27/(27-8) ...... 3^(inf+1)/(3^(inf+1)-2^(inf+1))
= 3 - 3^(inf+1)/(3^(inf+1)-2^(inf+1))
= 3 - 1 ( 3^(inf+1)/(3^(inf+1)-2^(inf+1)) = 1/(1 - (2/3)^(inf+1)) = 1)
= 2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-1-2006 11:15 PM
|
显示全部楼层
对了,其实还有另个解,用
6^k/(3^k-2^k)(3^k+1-2^k+1)
1/6{(3^k - 2^k)/(3^(k+1)-2^(k+1)) - (3^(k-1)-2^(k-1))/(3^k-2^k)} |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-1-2006 06:49 PM
|
显示全部楼层
平均数题目:
有101个整数,1到101。 你把他们分成两组A,B。A有m个数目,B有101- m 个数目。若40这数目从其中一组搬去另外一组,则A,B 的新平均数都比原来的大1/2。 请问 m 是多少? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-1-2006 08:01 PM
|
显示全部楼层
又一个 Method Of Differences 的题目
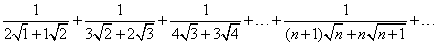
[ 本帖最后由 dunwan2tellu 于 25-1-2006 08:03 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-1-2006 09:23 PM
|
显示全部楼层
发表于 25-1-2006 09:23 PM
|
显示全部楼层
1/[(n+1)sqrt{n} + n(sqrt{n+1})]
= (n+1-n)/sqrt{n}sqrt{n+1}(sqrt{n}+sqrt{n+1})
= (sqrt{n+1}+sqrt{n})(sqrt{n+1}-sqrt{n})/sqrt{n}sqrt{n+1}(sqrt{n}+sqrt{n+1})
= (sqrt{n+1}-sqrt{n})/sqrt{n}sqrt{n+1}
= 1/sqrt{n} - 1/sqrt{n+1}
所以 E(n=1,inf) 1/[(n+1)sqrt{n} + n(sqrt{n+1})]
= 1/sqrt1 - 1/sqrt2 + 1/sqrt2 - 1/sqrt3 ......1/sqrt{n} - 1/sqrt{n+1}
= 1 - 1/sqrt{n+1}
= 1 (lim n->inf [1/sqrt{n+1}] = 0) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 6-2-2006 06:45 PM
|
显示全部楼层
设 a_k = (k^3-1)/(k^3+1)
那么
(i) S_n = (a_2)(a_3)(a_4)....(a_n) = ?
(ii) n->无限 S = ? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-2-2006 08:26 PM
|
显示全部楼层
这题比较难一点....
设 x_1 = 1 , x^2_{n+1}=(x_n)(x_n + 1)(x_n + 2)(x_n + 3)+1
求 1/(x_1 + 2) + 1/(x_2 + 2) + 1/(x_3 + 2) + ....
*提示:设 z_n = x_n + 1 ,然后证明 1/(z_k + 1) = 1/(z_k) - 1/(z_{k+1}) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-2-2006 08:49 PM
|
显示全部楼层
发表于 7-2-2006 08:49 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 6-2-2006 06:45 PM 发表
设 a_k = (k^3-1)/(k^3+1)
那么
(i) S_n = (a_2)(a_3)(a_4)....(a_n) = ?
(ii) n->无限 S = ?
a_k = (k^3-1)/(k^3+1)
= (k-1)(k^2+k+1)/(k+1)(k^2-k+1)
(i)(a_k)(a_k+1)(a_k+2)=(k-1)(k^2+k+1)/(k+1)(k^2-k+1) X (k+1-1)((k+1)^2+(k+1)+1)/(k+1+1)((k+1)^2-(k+1)+1) X (k+2-1)((k+2)^2+(k+2)+1)/(k+2+1)((k+2)^2-(k+2)+1)
=(k-1)(k^2+k+1)/(k+1)(k^2-k+1) X (k)(k^2+3k+3)/(k+2)(k^2+k+1) X (k+1)(k^2+5k+7)/(k+3)(k^2+3k+3)
=(k-1)(k)((k+2)(k+3)+1)/(k+2)(k+3)(k^2-k+1)
S_n = (2-1)(2)(n(n+1)+1)/n(n+1)(2^2-2+1)
= 2(n(n+1)+1)/3n(n+1)
(ii)S(n-->inf) = (2n^2+2n+2)/(3n^2+3n)
= 2/3 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-2-2006 09:23 PM
|
显示全部楼层
发表于 7-2-2006 09:23 PM
|
显示全部楼层
x^2_{n+1}=(x_n)(x_n + 1)(x_n + 2)(x_n + 3)+1
设x_n = a
x^2_{n+1}=a(a + 1)(a + 2)(a + 3)+1
=a^4+6a^3+11a^2+6a+1
x_{n+1} = sqrt{a^4+6a^3+11a^2+6a+1}
= a^2+3a+1
= (a+1)(a+2)-1
设 z_n = x_n + 1
1/(z_k + 1) = 1/[(x_k + 1) + 1]
= 1/(x_k + 2)
= (x_k + 1)/(x_k + 1)(x_k + 2)
= (x_k + 2 - 1)/(x_k + 1)(x_k + 2)
= 1/(x_k + 1) - 1/(x_k + 1)(x_k + 2) - 1 + 1
= 1/z_k - 1/z_{k+1}
1/(x_1 + 2) + 1/(x_2 + 2) + 1/(x_3 + 2) + ....
= 1/(z_1 + 1) + 1/(z_2 + 1) + 1/(z_3 + 1) + ....
= 1/z_1 - 1/z_2 + 1/z_2 - 1/z_3 + 1/z_3 - 1/z_4 + ....
= 1/z_1
= 1/(x_1 + 1)
= 1/2
[ 本帖最后由 hamilan911 于 10-2-2006 09:32 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 9-2-2006 03:15 PM
|
显示全部楼层
|
hamilan911 , 建议你下次用mathtype 打solution 吧!如果没有看漏的话,应该是对了。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 3-3-2006 05:52 PM
|
显示全部楼层
反三角函数级数题:
证明 arctan (1/(2k^2)) = arctan (2k+1) - arctan(2k-1) ,之后
求 sum_{k=1 to 无限} arctan(1/(2k^2)) = ? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-3-2006 04:58 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|