|
|

楼主 |
发表于 12-10-2004 10:11 AM
|
显示全部楼层
28/09/2004,星期二
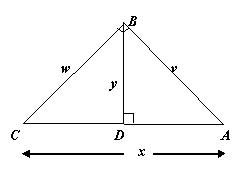
初中(A20) 如图,角 ABC 及 角 BDA 皆是直角。
若 v + w = 35,x + y = 37,
求 y 之值。
 (已解) (已解)
(答案:12)
(解对者:eeCyang)
已知,v + w = 35,x + y = 37
角 ABC ,x^2=w^2+v^2
角 ABC 及 角 BDA 的面积相同,xy/2=wv/2
x^2=w^2+v^2
x^2=(w+v)^2-2wv
x^2+2wv=35^2
x^2+2xy=35^2(xy=wv)
(x+y)^2-y^2=35^2
所以,y^2=37^2-35^2
y^2=144
y=12(-ve value 不合题意)
[ Last edited by pipi on 12-10-2004 at 11:43 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:11 AM
|
显示全部楼层
29/09/2004,星期三
初中(A21) 若 x < -2,试简化 |1-|1+x||。 (已解)
(答案:-2-x)
(解对者:eeCyang)
x < -2
1+x<-1
|1+x|=-(1+x),1+x<-1
1-[-(1+x)]=1+(1+x)
1+(1+x)<0 , (1+x<-1)
|1-|1+x||=-(1+1+x)=-2-x
[ Last edited by pipi on 12-10-2004 at 11:44 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:21 PM
|
显示全部楼层
04/10/2004,星期一
初中(A22) 当 1956, 1980 及 2004 除一正整数 a ,其余数均为 b 。
求 a + b 的最大值。 (已解)
(答案:36)
(解对者:38女)
1980 - 1956 = 24
2004 - 1956 = 48
gcd(24,48) = 24
因此,12 ≡ 1956 (mod 24)
≡ 1980 (mod 24)
≡ 2004 (mod 24)
a = 24;b = 12
a + b = 36
[ Last edited by pipi on 12-10-2004 at 12:29 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:21 PM
|
显示全部楼层
05/10/2004,星期二
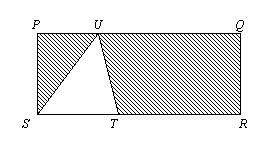
初中(A23) 如图, PQRS 为一长方形。已知 PQ = 3 PS,ST:SR = 1:3 。
求 三角形 SUT 的面积 和 阴影部分面积 之比。
 (已解) (已解)
(答案:1 : 5)
(解对者:史奴比{^_^})
若把PS=k, PQ = 3k
那么,PQRS 面积 = 3k^2
ST : SR = PS : PQ (SR=PQ, ST=PS)
= 1 : 3
SUT 面积 = 1/2 k^2(ST*PS)
阴部分面积 = PQRS 面积 - SUT 面积
= (3 - 1/2) k^2
= 5/2 k^2
那么,SUT 面积 : 阴部分面积 = (1/2) : (5/2)
= 1 : 5
[ Last edited by pipi on 12-10-2004 at 12:30 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:21 PM
|
显示全部楼层
06/10/2004,星期三
初中(A24) 已知 a = x + 1
b = x + 2
c = x + 3
求 a^2 + b^2 + c^2 - ab -bc - ca 之值。 (已解)
(答案:3)
(解对者:38女?放?葅^_^},止战之殇,灰羊,sMIL3)
解法(一)
b = a + 1; c = a + 2
a^2 + b^2 + c^2 - ab -bc - ca
= a^2 + (a + 1)^2 + (a + 2)^2 - a(a + 1) - (a + 1)(a + 2) - (a + 2)a
= a^2 + a^2 + 2a + 1 + a^2 + 4a + 4 - a^2 - a - a^2 -3a - 2 - a^2 - 2a
= 1 + 4 - 2
= 3
解法(二)
(a-b)^2 = a^2 + b^2 - 2ab
(b-c)^2 = b^2 + c^2 - 2bc
(c-a)^2 = c^2 + a^2 - 2ca
(a-b)^2 + (b-c)^2 + (c-a)^2 = 2a^2 + 2b^2 + 2c^2 - 2ab - 2bc - 2ca
除以2 :
[(a-b)^2 + (b-c)^2 + (c-a)^2]/2 = a^2 + b^2 + c^2 - ab - bc - ca (如题目所要的)
a-b = -1, b-c = -1 , c-a = 2
答案: a^2 + b^2 + c^2 - ab - bc - ca = [(-1)^2 + (-1)^2 + (2)^2]/2
= 6/2
= 3
解法(三)
ab = (x + 1)(x + 2)
= x^2 + 3x + 2
bc = (x + 2)(x + 3)
= x^2 + 5x +6
ac = (x + 1)(x + 3)
= x^2 + 4x + 3
(a + b + c)^2 = a^2 + b^2 c^2 + 2ab + 2bc + 2ac
a^2 + b^2 c^2 = (a + b + c)^2 - 2ab - 2bc - 2ac
= (3x + 6)^2 - 2ab - 2bc - 2ac
= 9x^2 + 36x + 36 - 2ab - 2bc - 2ac
= 3(3x^2 + 12x + 12) - 2ab - 2bc - 2ac
= 3(ab + bc + ac) + 3 - 2ab - 2bc - 2ac
= 3 + ab + bc + ac
a^2 + b^2 + c^2 - ab -bc - ca
= 3 + ab + bc + ac - ab -bc - ca
= 3
解法(四)
a^2+b^2+c^2-ab-bc-cd
=a(a-b) + b(b-c) + c(c-a)
=2c-a-b
=3
[ Last edited by pipi on 12-10-2004 at 12:32 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:22 PM
|
显示全部楼层
11/10/2004,星期一
初中(A25) 若 a/b = b/c = c/d = d/a ,其中 abcd ≠0。
求 (a+b+c+d)/(a+b+c-d) 之值。 (已解)
(答案:0 或 2)
(解对者:史奴比{^_^},430201)
解法(一)
a/b = d/a b/c = c/d
a^2 = bd c^2 = bd
a^2 = c^2 = bd
a = c = +/- (bd)^1/2
a/b = b/c c/d = d/a
b^2 = ac d^2 = ac
b^2 = d^2 = ac
b = d = +/- (ac)^1/2
(a+b+c+d)/(a+b+c-d) = (2a + 2b)/(2a)
= 1 + b/a
= 1 + b / [+/- (bd)^1/2]
= 1 + (b/d)^1/2 @ 1 - (b/d)^1/2
= 1 + 1 @ 1 - 1
= 2 @ 0
解法(二)
設 a/b = b/c = c/d = d/a=k(k為常數)
則a=bk,b=ck,c=dk,d=ak
即a=ck^2=dk^3=ak^4
∵a≠0,∴k^4=1→k=±1
(1)若k=1
則a=b=c=d
故(a+b+c+d)/(a+b+c-d)=(4a)/(2a)=2(∵a≠0)
(2)若k=-1
則b=-a,c=a,d=-a
故(a+b+c+d)/(a+b+c-d)=0/(2a)=0(∵a≠0)
[ Last edited by pipi on 21-10-2004 at 11:47 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:23 PM
|
显示全部楼层
12/10/2004,星期二
初中(A26) 已知 A,B,C,D,E 为整数,且 0 ≤A,B,C,D,E≤9 。
若 A B C D E
x 4
_________________
E D C B A
----------
求 A,B,C,D,E 之值。 (已解)
(答案:(A,B,C,D,E)=(2,1,9,7,8))
(解对者:史奴比{^_^},灰羊,38女)
解法(一)
4的乘法表 : 0 1 2 3 4 5 6 7 8 9
--> 0 4 8 12 16 20 24 28 32 36
从A,E做起,
A x 4 = E (个位数) E x 4 = *A
A = 1 or 2 --> = *1 or *2 (个位数是1或2)
(不可能是0,A不等于E) E = - or 3/8
If E=3, A=1
那么 A x 4 = E
1 x 4 + (9) = 13
-> 不可能 A=1, E=3, 1) 4 的乘法表最多能进位到3而已。
2) A x 4 只得单数。
所以可以确定,A=2, E=8
2***8 x 4 = 8***2
接下来找B, D,
B x 4 = D (单数,没进位) D x 4 + (3) = *B (8x4 = 32, 进3)
B = 0 or 1 or 2 = *0 or *1 or *2
(个位数是0或1或2)
D = - or 2/7 or -
B 肯定是 = 1 (D不可能是2 , D不等于A)
所以 D=7
最后找 C
D x 4 + (3) = 31 (进位3)
C x 4 + (3) = 3C 为何3C ? --> B x 4 = D
1 x 4 + (3) = 7
( 需要从 C x 4 进位(3))
所以结果 C 只能等于 9
答案:21978 x 4 = 87912 (若A B C D E 不重复)
解法(二)
首先,A一定小於3,不然乘出來是六位數
∴A=2(因為E*4不會得到個位數1) => E=8
B也一定小於3,不然A*4不會得E,
考慮B≠2,因為上面E*4後會進位3,所以B一定是奇數
∴B=1 => D=7 (因為D*4後加上進位的3得到個位數1,且D>4)
D=7,所以上面D*4後加上進位的3=31,進位3,
0≤C≤9,且C*4加上進位的3後.會進位3
∴C=9
(A,B,C,D,E)=(2,1,9,7,8)
解法(三)
由题目,知道A<E,而且A*4一定会是个位数,因此A只能是1或2.A若是1的话,E就是4了,而E*4不等于A=1.
因此,A=2;E=8.
接着B*4也一定是个位数,也知道B<D.由于A=2;E=8,那E*4=8*4=32,进位3.
D*4+3的个位数要小于D.因此D只能是7,7*4+3=31,所以B=1,进位3.
然后,C*4+3的个位数要是C,因此只有C=9,因为9*4+3=39.C=9,进位3.
最终的答案便是:
21978
x 4
---------
87912
---------
[ Last edited by pipi on 19-10-2004 at 10:22 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-10-2004 10:14 AM
|
显示全部楼层
13/10/2004,星期三
初中(A27) 甲、乙兩人轮流报数,必须报不大於2的自然数,把兩人报的数加起來,
谁报数后加起來的数是20,谁就获胜。
如甲要取胜,是先报还是后报?报几?(请解释你的论点!) (已解)
(答案:甲先报。报 2)
(解对者:灰羊,fritlizt,38女)
解法(一)
甲先報!報2,接下來對方報2甲就報1,對方報1甲就報2,甲必勝!
因為報的數必須是1或2,所以每一次
甲跟乙報的數的和一定可以湊成3
3*6=18,甲如果先報2,解下來把自己報的數
和乙報的數湊成3,哪麼甲第7次報數就能湊成3*6+2=20
就能勝利了!
解法(二)
先报数的赢。报 2 号。
如果先报到 20 号的赢。也就是说报17号的赢了。
如此推算,报2号的赢定。
解法(三)
先报,而且要报到2,然后报(2+3),再报(2+3+3),(2+3+3+3)...
[ Last edited by pipi on 19-10-2004 at 10:21 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:51 PM
|
显示全部楼层
18/10/2004,星期一
初中(A28) 100 个学生排成一列,由左到右,报数!
1,2,3,...,100。
现在喊奇数的学生退出;喊偶数的学生保留,然后由左到右,报数!
1,2,3,...,50。
现在喊奇数的学生退出;喊偶数的学生保留,然后由左到右,报数!
1,2,3,...,25。
。。。
如此指令重复,直到最后一个学生!
问:这最后一个学生第一次喊什么号码? (已解)
(答案:64)
(解对者:430201,史奴比{^_^})
解法
第一次剩下2的倍數:2、4、6、8、…、100
第二次剩下4的倍數:4、8、12、16、…、100
第三次剩下8的倍數:8、16、24、32、…、96
第四次剩下16的倍數:16、32、48、64、80、96
第五次剩下32的倍數:32、64、96
第六次剩下64的倍數:64
[ Last edited by pipi on 25-10-2004 at 04:00 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:54 PM
|
显示全部楼层
19/10/2004,星期二
初中(A29) 若 1/a + 1/b + 1/c = 1/(a+b+c),
求证 a^3 + b^3 + c^3 = (a+b+c)^3。 (已解)
(答案:--)
(解对者:多普勒效应,430201)
解法(一)
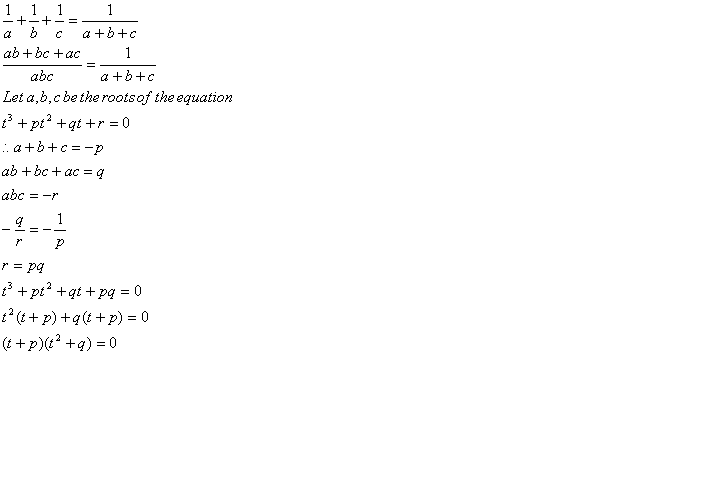
所以,a,b,c 中必有两个是相反数。
设 a=-b
所以
a^3 + b^3 + c^3 = c^3
(a+b+c)^3 = c^3
所以 a^3+b^3+c^3 = (a+b+c)^3
解法(二)
已知 1/a + 1/b + 1/c = 1/(a+b+c),
去分母化簡得a^2×b+a×b^2+b^2×c+b×c^2+c^2×a+c×a^2=-2abc
又(a+b+c)^3=a^3+b^3+c^3+3(a^2×b+a×b^2+b^2×c+b×c^2+c^2×a+c×a^2)+6abc
得(a+b+c)^3-(a^3 + b^3 + c^3)=3(a^2×b+a×b^2+b^2×c+b×c^2+c^2×a+c×a^2)+6abc=3×(-2abc)+6abc=0
故a^3 + b^3 + c^3 = (a+b+c)^3
解法(三)
已知 1/a + 1/b + 1/c = 1/(a+b+c),去分母得
(a+b+c)(ab+bc+ca)=abc
﹝(a+b)+c﹞(ab+bc+ca)-abc=0
(a+b)(ab+bc+ca)+c(ab+bc+ca)-abc=0
(a+b)(ab+bc+ca)+c^2(a+b)=0
(a+b)(ab+bc+ca+c^2)=0
(a+b)﹝b(a+b)+c(a+c)﹞=0
(a+b)(b+c)(c+a)=0
則a=-b或b=-c或c=-a
分別以a=-b或b=-c或c=-a代入
a^3 + b^3 + c^3 = (a+b+c)^3
的左右兩式即得證
[ Last edited by pipi on 25-10-2004 at 04:02 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:54 PM
|
显示全部楼层
20/10/2004,星期三
初中(A30) 小明将 1,2,3,4,5,6,7,8,9 分别写在3X3的表格内(如下图),每格一个数字。
他分别将各(横)行,和各(竖)列的三个数加起来。
把和写在表的下方和右方。
试找出 * 之值。
 (已解) (已解)
(答案:7)
(解对者:多普勒效应,430201,史奴比{^_^})
解法(一)

解法(二)
借用樓上的A、B、C、D、E、F、G、H、I,謝謝!!
∵(A+D+G)+(D+E+F)=23+21=44
又A+D+G+E+F的最大值為(9+8+7+6+5=)35
∴D=9,且A、G、E、F必為5、6、7、8之一。
而B、C、H、I必為1、2、3、4之一。
∵C+F+I=8,且F為5、6、7、8之一 C、I為1、2、3、4之一。
∴F=5,則E=21-9-5=7,
解法(三)
先找出最大的和数。
23 = 9 + 8 + 6 (只有唯一的选择)
21 = 9 + 7 + 5 或者 8 + 7 + 6
但是 若用 8 + 7 + 6, 那么将会出现两个数字重复,
所以 只有 21 = 9 + 7 + 5
9 将会重叠, 所以9 一定要在上中间。
现在 7 和 5 的位置 就要考虑放在哪里。
若把 5 放中间,那么
14 = 8 + 5 + 1 / 7 + 5 + 2 / 6 + 5 + 3 / 4 + 5 + 6 /
6,7,8,9 已经用过了
那么看来以上的都不可以用。
所以只有 7 可以摆中间。
1, 2, 3, 4, 就如以下添进去
8 9 6 | 23
4 7 3 | 14
1 5 2 | 8
-----------------------
13 21 11
* 当然是 7。
[ Last edited by pipi on 25-10-2004 at 04:04 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:35 PM
|
显示全部楼层
25/10/2004,星期一
初中(A31) 若 (a+b)/(a-b) = 7/4
求 (a^2)/(b^2) 之值。 (已解)
(答案:121/9)
(解对者:多普勒效应,430201)
解法(一)
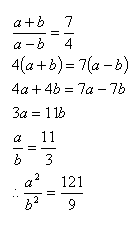
解法(二)
∵(a+b)/(a-b) = 7/4
利用合分比性質
∴〔(a+b)+(a-b)〕/〔(a+b)-(a-b)〕=(7+4)/(7-4)
則a/b=11/3
故(a^2)/(b^2) 之值為121/9。
[ Last edited by pipi on 30-10-2004 at 07:54 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:36 PM
|
显示全部楼层
26/10/2004,星期二
初中(A32) 已知 六位数 174xyz 能被 7,11,13 整除。
求 x + y + z 。 (已解)
(答案:12)
(解对者:430201,史奴比{^_^})
解法(一)
已知 六位数 174xyz 能被 7,11,13 整除。
所以 六位数 174xyz 必能被 7,11,13的最小公倍數1001 整除。
顯然 六位数 174xyz ÷1001=174
則 x=1,y=7,z=4。
故 x + y + z=12
[ Last edited by pipi on 30-10-2004 at 07:55 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:36 PM
|
显示全部楼层
27/10/2004,星期三
初中(A33) 在某一数,x 的前后各添上"1"。
得到的数 y, 比 x 大 13439。
求 x 。 (已解)
(答案:382)
(解对者:多普勒效应,430201,史奴比{^_^})
解法(一)

解法(二)
設x為(n-1)位數,n>1
(10^n+10x+1)-x=13439
x=(13438-10^n)/9>0
則n<5
(1)若n=2,則x=1482(不合)
(2)若n=3,則x=1382(不合)
(3)若n=4,則x=382
解法(三)
x 前后添 1 , 那么就是 1"x"1
y - x = 13439
1"x"1
- "x"
--------- ==> x 应该是3位数, abc
13439
---------
所以 1 a b c 1
- a b c
--------------
1 3 4 3 9
--------------
以最快方法添进去,
c = (1)1 - 9 = 2 (1,需要借位)
b = (1)2 - *1* - 3 = 8 (1,需要借位 / *1* 被借位)
a = 8 - *1* - 4 = 3
x = 382
[ Last edited by pipi on 30-10-2004 at 07:57 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 31-10-2004 10:19 PM
|
显示全部楼层
发表于 31-10-2004 10:19 PM
|
显示全部楼层
01/11/2004,星期一
初中(A34)
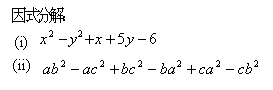
(答案:(x+y-2)(x-y+3),(a-b)(b-c)(c-a))
(解答者:430201)
解法
1、原式=(x+y)(x-y)+(x+5y)-6
=(x+y-2)(x-y+3)
2、原式=(ab^2-ac^2)-(cb^2-bc^2)-(ba^2-ca^2)
=a(b+c)(b-c)-bc(b-c)-a^2(b-c)
=(b-c)(ab+ca-bc-a^2)
=(b-c)﹝c(a-b)-a(a-b)﹞
=(a-b)(b-c)(c-a)
[ Last edited by 多普勒效应 on 5-11-2004 at 08:50 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 31-10-2004 10:20 PM
|
显示全部楼层
发表于 31-10-2004 10:20 PM
|
显示全部楼层
02/11/2004,星期二
初中(A35)
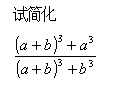
(答案:(2a + b)/(a + 2b))
(解答者:chiaweiwoo1)
((a + b)^3 + a^3 )/(a + b)^3 + b^3)
= ((2a + b)((a + b)^2 - (a + b)(a) + a^2)/((a + 2b)((a + b)^2 - (a + b)(b) + b^2)
= (2a + b)(a^2 + 2ab + b^2 - a^2 - ab + a^2)/
(a + 2b)(a^2 + 2ab + b^2 - b^2 - ab + b^2)
= (2a + b)(a^2 + ab + b^2)/
(a + 2b)(a^2 + ab + b^2)
= (2a + b)/(a + 2b)
[ Last edited by 多普勒效应 on 5-11-2004 at 08:49 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-11-2004 08:54 PM
|
显示全部楼层
发表于 5-11-2004 08:54 PM
|
显示全部楼层
03/11/2004,星期三
初中(A36)
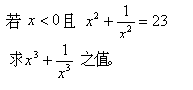
(答案:)
(解对者:430201,史奴比{^_^})
解法(一)
( x + 1/x )^2 = x^2 + 1/x^2 + 2
已知 :x^2 + 1/x^2 = 23
所以 ( x + 1/x )^2 = 23 + 2
= 25
( x + 1/x ) = 5 @ -5
但是 x < 0 , ( x + 1/x ) 不可能等于 5
所以,( x + 1/x ) = -5
( x + 1/x )^3 = x^3 + 1/x^3 + 3( x + 1/x)
x^3 + 1/x^3 = ( x + 1/x )^3 - 3( x + 1/x)
= (-5)^3 - 3(-5)
= -125 + 15
= -110
解法(二)
∵x^2+(1/x)^2=23
∴(x+1/x)^2=x^2+2+(1/x)^2=25
但x<0,則x+1/x=-5
故x^3+(1/x)^3=(x+1/x)〔x^2-1+(1/x)^2〕=(-5)×(23-1)=-110 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:37 AM
|
显示全部楼层
发表于 19-11-2004 12:37 AM
|
显示全部楼层
08/11/2004,星期一
初中 (A37)
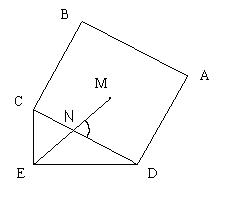
ABCD 是正方形,CED是直角三角形。
M是ABCD的中点,D=60度,求角MND之值。
(已解)
(答案:105度)
(解对者:430201)
1、連CM、DM,
則∠CMD=90度,且CM=DM,∴∠MCN=45度。
2、∵∠CMD=90度,∠CED=90度,
∴C、E、D、M四點共圓
則∠CMN=∠CDE=60度
故∠MND=∠CMN+∠MCN=105度
[ Last edited by 多普勒效应 on 19-11-2004 at 12:43 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:41 AM
|
显示全部楼层
发表于 19-11-2004 12:41 AM
|
显示全部楼层
09/11/2004,星期二
初中 (A38)

(已解)
(答案:2)
(解对者:萧晨,430201)
解法(一)
=2^(2/3) + 2^(1/3) +1
(2^(1/3)-1)x=(2^(1/3)-1)(2^(2/3) + 2^(1/3) +1)=1--------->(a-1)(aa+a+1)=a^3-1
(2^(1/3)-1)=1/x
2^(1/3)=1+1/x
解法(二)
1+1/x=(x+1)/x=〔2^(2/3) + 2^(1/3) +1+1〕/〔2^(2/3) + 2^(1/3) +1〕
=1+〔2^(1/3) -1〕(有理化分母,即分子、分母同乘以〔2^(1/3) -1〕)
=2^(1/3)
故(1+1/x)^3=2
左右三次方-->2=(1+1/x)^3 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:47 AM
|
显示全部楼层
发表于 19-11-2004 12:47 AM
|
显示全部楼层
10/11/2004,星期三
初中 (A39)
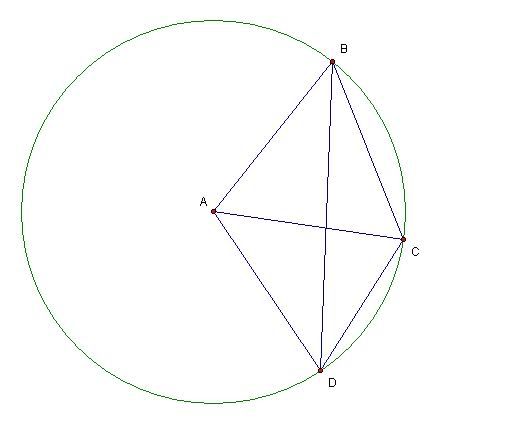
ABCD是凸四边形,且AB=BC=AC=AD,
求角BDC之值。
(已解)
(答案:30度)
(解对者:fritlizt,430201,萧晨)
解法(一)
ABC等边三角形
ABD等腰三角形
所以可以花在一个圆圈里面
BCD在圆周
A是圆心
然后利用圆心角=2x圆周角
BAC角=2BDC角---〉以BC为底
然后就知道BDC角度是60/2=30度了
解法(二)
∵AB=AD
∴設∠ABD=∠ADB=a度,
則∠BAD=(180-2a)度
∵AB=BC=CA
∴∠BAC=60度
則∠CAD=∠BAD-∠BAC=(120-2a)度
∵AC=AD
則∠ADC=(180-120+2a)/2度=(30+a)度,
故∠BDC=∠ADC-∠ADB=30度 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|