|
|
看到个不错的题目,就贴上来分享。
求 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
分母部分是所有只能被 2 和 3 整除的数目。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-11-2005 03:38 PM
|
显示全部楼层
之后也可以试看把他generalised 到可以被n个质数整除的和。
E.g : 被 2,3,5,7 整除。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-11-2005 04:22 PM
|
显示全部楼层
发表于 24-11-2005 04:22 PM
|
显示全部楼层
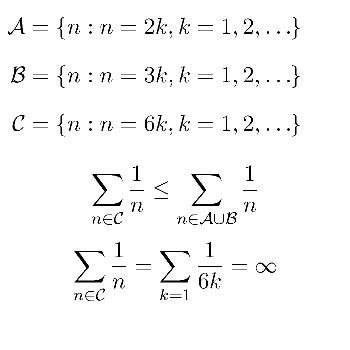
怎么会收敛呢? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-11-2005 05:28 PM
|
显示全部楼层
|
铁蛋兄,注意哦,是只能被 2,3 整除。而不是所有被2,3 整除。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-11-2005 10:51 AM
|
显示全部楼层
发表于 25-11-2005 10:51 AM
|
显示全部楼层
原帖由 dunwan2tellu 于 24-11-2005 05:28 PM 发表
铁蛋兄,注意哦,是只能被 2,3 整除。而不是所有被2,3 整除。
dunwan2tellu 网友, 如果不是所有被2,3 整除,那么我们怎么知道下一个该加的号码该是什么?如你给的前面几个号码,
原帖由 dunwan2tellu 于 24-11-2005 03:32 PM 发表
看到个不错的题目,就贴上来分享。
求 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
分母部分是所有只能被 2 和 3 整除的数目。
1/10 并没在里面(虽然 10 可被 2 整除)。那 1/12 下一个号码是什么?是 1/14?还是 1/15?还是 1/16? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-11-2005 06:33 PM
|
显示全部楼层
flash 兄, 10 不在里面因为他也可以被 5 整除。这表示它不是只能被 2 整除。为了方便明白,所有的分母都是 2^a 3^b , a,b>=0 的pattern .  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-11-2005 07:43 PM
|
显示全部楼层
发表于 25-11-2005 07:43 PM
|
显示全部楼层
设S = 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
所以S = 1 + 1/2 S + 1/3 S - 1/6 S
S = 1 + 2/3 S
1/3 S= 1
S = 3 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-11-2005 07:46 PM
|
显示全部楼层
|
赞! hamilan911 ! 对了。我的做法是用 GP 的,不过我喜欢你的做法! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-11-2005 11:43 PM
|
显示全部楼层
|
有没有人要试试我所说的GP的方法呢?还是其他的方法呢?这题可以generalise 哦。E.g : 求所有分母为 p1^(a1)p2^(a2)...pn^(an),ai =>0 ,pi为质,分子为 1 ,的级数。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2005 01:28 PM
|
显示全部楼层
发表于 26-11-2005 01:28 PM
|
显示全部楼层
看起来是对可是记得 S 是 infinite series.
1/2 S + 1/3 S - 1/6 S 里的项到底要怎么排呢?如果是多项式就没有问题,可是S是 infinite series, 在计算有负值的 infinite series 秩序很重要,因为如果秩序不重要那总可以找到一些项的组合使到这个 infinite series 收敛或发散.
利用多项式的解法于infinite series, 在理论方面有问题。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 26-11-2005 01:53 PM
|
显示全部楼层
会吗?这方法就像集合里 P(AUB) = P(A) + P(B) - P(A N B) .应该不会有那个特别状况吧? 这应该不会和那 1-1+1-1+1....=0 或 1 的问题相同的。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2005 03:13 PM
|
显示全部楼层
发表于 26-11-2005 03:13 PM
|
显示全部楼层
S 每一项的式是 1/(2^x 3^y).
A = {(x,y)} = {(0,0), (1,0), (0,1), (2,0), (1,1), (3,0), (0,2), (2,1), (4,0), (1,2), ....}
注意: {(0,1), (1,1), (2,1), (3,1), .... } 是 A 的子集. 可是
1/3 + 1/6 + 1/12 + 1/24 + ... ≤ 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/12 + 1/16 + 1/18 + 1/24 + ...
然而左边不收敛,.所以我对之前的解有怀疑。
[ 本帖最后由 铁蛋 于 26-11-2005 03:15 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 26-11-2005 10:55 PM
|
显示全部楼层
发表于 26-11-2005 10:55 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-11-2005 01:02 PM
|
显示全部楼层
发表于 27-11-2005 01:02 PM
|
显示全部楼层
原帖由 hamilan911 于 25-11-2005 07:43 PM 发表
设S = 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
所以S = 1 + 1/2 S + 1/3 S - 1/6 S
S = 1 + 2/3 S
1/3 S= 1
S = 3
S = 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
怎樣變成S = 1 + 1/2 S + 1/3 S - 1/6 S
???? |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 27-11-2005 09:37 PM
|
显示全部楼层
我的是酱解
分母是 2^a 3^b , a,b>= 0
当 a 是任何非零整数时 ,b 可以是 0 到 无限。所以它们的和是
(sum 1/2^a )(sum 1/3^b) = 2 x 3/2 = 3
*上面的是两个等比无穷级数的积。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 27-11-2005 10:40 PM
|
显示全部楼层
回铁蛋#12
左边是等比无穷级数 ,a=1/3 , r=1/2 所以当然收敛到 2/3 .我不明白你想表达的是什么? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-11-2005 11:51 AM
|
显示全部楼层
发表于 28-11-2005 11:51 AM
|
显示全部楼层
 很抱歉看花了眼! 很抱歉看花了眼! 人老了越来越糊涂 人老了越来越糊涂
分母值
x
y 0 1 2 3 4 5
0 1 2 4 8 16 32 ...
1 3 6 12 24 48 96 ...
2 9 18 36 72 144 288 ...
3 27 ..................................
4 81 ..................................
. .
. .
. .
每一排都可以 factorize 出一个无穷几何和 1 + 1/2 + 1/4 + ... = 2.
而这个每一排都会乘上 1, 1/3 , 1/9 , ... 故有
(1 + 1/3 + 1/9 + ... ) * 2 = 3 .
hamilan911 虽然得到一样的答案,可是必须先证明 S 是收敛的,那 S 就是一个常数,这样他的作法才成立。如果 S 不收敛,那这个做法肯定不成立。所以要使到它严谨就必需附上S收敛的证。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 28-11-2005 07:49 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-11-2005 12:48 PM
|
显示全部楼层
发表于 29-11-2005 12:48 PM
|
显示全部楼层
原帖由 hamilan911 于 25-11-2005 07:43 PM 发表
设S = 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + ....
所以S = 1 + 1/2 S + 1/3 S - 1/6 S
S = 1 + 2/3 S
1/3 S= 1
S = 3
不明白…有谁可以解释吗?
如果s是infinite series的话…还是想不通… |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-11-2005 03:44 PM
|
显示全部楼层
发表于 29-11-2005 03:44 PM
|
显示全部楼层
S = 1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + 1/16 + 1/18 + 1/24 + 1/27 + 1/32 + 1/36......
= 1 + 1/2(1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + 1/18....) + 1/3(1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + 1/18....) - 1/6(1 + 1/2 + 1/3 + 1/4 + 1/6 + 1/8 + 1/9 + 1/12 + 1/18....)
= 1 + 1/2S + 1/3S - 1/6S
酱解释会较清楚吧,其实这就是用到那个set的P(AUB) = P(A) + P(B) - P(A N B) |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|