|
查看: 6003|回复: 75
|
数学训练(十二月份)
[复制链接]
|
|
|
12月份的就由微中子主持吧.
以下的问题都是多普勒提供的.
十一月未解
高中 (B39)
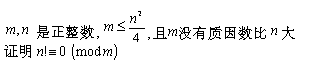
高中 (B40)
解联立方程:
X_i 是实数
X_1 + X_2 + ... + X_1999 = 1999
(X_1)^4 + (X_2)^4 + ... + (X_1999)^4 = (X_1)^3 + (X_2)^3 + ... + (X_1999)^3
(已解)
(答案:X_i = 1)
(解对者:kee020041)
高中 (B41)
a_i 是正整数 i=1,2,3,...,n
已知 a_1 + a_2 + ... + a_n = 2002
求 (a_1)(a_2)...(a_n)的最大值。
高中 (B42)
i,j是正整数,
当 i,j 属于 S ,则 (i+j)/gcd(i,j) 属于 S
找出所有有限非空集 S
[ gcd(a,b) 表示 a,b 的最大公因数 ]
十二月
01/12/2004 星期三
初中(A45)
log_{2} 3 = a
3^{b} = 7
求 log_{12} 56
(已解)
(答案:3+ab)/(2+a) )
(解对者:灰羊)
02/12/2004 星期四
高中(B43)
60^{a} = 3 , 60^{b} = 5
求 12^{(1-a-b)/(2-2b)}
(已解)
(答案:2)
(解对者:灰羊)
03/12/2004 星期五
高中(B44)
在三角形ABC中,若sin C = cos A + cos B,
求证三角形ABC为直角三角形.
(已解)
(答案:--)
(解对者:灰羊)
04/12/2004 星期六
高中(B45)
A , B是正整数,且A^2 + B^2 = 15
A^3 + B^3 = 28
问共有几组(A,B)
(已解)
(答案:0)
(解对者:430201)
05/12/2004 星期日
大专(C16)
问,共有几个整数n在1和2003之间使1^{n} + 2^{n} + 3^{n} + 4^{n} + 5^{n}可以被5整除.
(待解)
(答案:)
(解对者:)
06/12/2004 星期一
初中(A46)
考虑 1^1, 2^2, 3^3, 4^4, ...这个数列.
1^1 = 1, 2^2 = 4, 3^3 = 27, 4^4 = 256,
如果我们拿最后一个数字来组成新的数列1,4,7,6,...
如果无限的做下去,有什么pattern?
(待解)
(答案:)
(解对者:)
07/12/2004 星期二
初中(A47)
写出以下算式:
* *
x * *
---------------
* * *
* * *
---------------
* * * *
+ 1 * *
---------------
* * * * *
---------------
*代表0到9中任何一个数字,不需是一样的.
就是写出每一个*代表什么数字.
(已解)
(答案:)
(解对者:灰羊)
08/12/2004 星期三
初中(A48)
已知x,y,z为正数且2^x = 3^y = 5^z.
那么2x, 3y, 5z何者为大,何者为小.
(已解)
(答案:5z 最大)
(解对者:chwk87,430201)
09/12/2004 星期四
高中(B46)
找出所有domain是实数的涵数,符合:
1. f(1)=1
2. f(x_1 + x_2)=f(x_1)+f(x_2)
3. f(1/x) = 1/x^2 f(x), x不等于0.
(已解)
(答案:f(x)=x)
(解对者:灰羊)
10/12/2004 星期五
高中(B47)
如果两个正数之间的和数小于它们之间的积数,证明它们的和大于4.
(待解)
(答案:)
(解对者:)
11/12/2004 星期六
高中(B48)
如果把正整数依照次序写到1990,我们可以得到
S0 = 123456789101112131415…19891990
现在,把第2,4,6,8…的数字删除,我们可得
S1 = 1357901234…9990
再把第1,3,5,7…的数字删除。
S2 = 37024…
我们继续以上两个步骤,
S3由S2的第2,4,6,8…数字被删除后形成,
S4由S3的第1,3,5,7…数字被删除后形成。
请问剩下一个数字的时候,那个数字是什么?
(待解)
(答案:)
(解对者:)
13/12/2004 星期一
初中(A49)
从 1 开始的若干个连续自然数的和等于一个各位数字相同的三位数(每个数字都一样)。问,应取几个连续自然数?
(已解)
(答案:36)
(解对者:430201,灰羊)
14/12/2004 星期二
初中(A50)
求方程 xyz=5(x+y+z)的正整数解,并且 x,y,z是质数。
(已解)
(答案:2,5,7 )
(解对者:430201,灰羊[答对1/6] ) )
15/12/2004 星期三
初中(A51)
A B C D E
2 5 8
23 20 17 14 11
26 29 32
47 44 41 38 35
......
数字 2000会出现在那一列?
(待解)
(答案:)
(解对者:)
16/12/2004 星期四
高中(B49)
解方程
3^(2x) - 34[15^(x-1)] + 5^(2x) = 0
(已解)
(答案:)
(解对者:灰羊)
17/12/2004 星期五
高中(B50)
a,b 是正整数,
若 a+b = 30030
证明 ab 不可以被 30030 整除。
(已解)
(答案:-)
(解对者:灰羊)
18/12/2004 星期六
高中(B51)
三角形 ABC 中,AB = AC,角 BAC=20度
D,E 分别是AB,BC上一点 ,使角DCB = 50度,角EBC=60都
求角BED之值。
(待解)
(答案:)
(解对者:)
20/12/2004 星期一
初中(A52)
x 为何值时, f(x)=(x - a_1)^2 + (x - a_2)^2 + ... + (x-a_n)^2
取最小值?
(已解)
(答案:x=(a_1+a_2+…+a_n)/n)
(解对者:430201)
21/12/2004 星期二
初中(A53)
化简
√[x + 4√(x+1) +5] + √[x + 6√(x+1) + 10]
(已解)
(答案:2√(x+1)+5 )
(解对者:430201)
22/12/2004 星期三
初中(A54)
已知 (y+z)/(b-c) = (x+z)/(c-a) = (x+y)/(a-b) > 0
a,b,c 互不相等,且都不等于零。
求证,以上各分式都等于
√{[x^2+y^2+z^2]/[(b-c)^2+(c-a)^2+(a-b)^2]}
(已解)
(答案:-)
(解对者:430201)
23/12/2004 星期四
高中(B52)
化简
3/(1!+2!+3!) + 4/(2!+3!+4!) + ... + 2001/(1999!+2000!+2001!)
(已解)
(答案:)
(解对者:430201)
24/12/2004 星期五
高中(B53)
证明,一个有 n 个元素的集合有 2^n 个子集。
(已解)
(答案:-)
(解对者:灰羊,430201)
我的数学造诣不会比各位高,所以如果发现答案有错误,请指出.谢谢
[ Last edited by 多普勒效应 on 27-12-2004 at 04:35 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 01:05 PM
|
显示全部楼层
发表于 3-12-2004 01:05 PM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
03/12/2004 星期五
高中(A44)
在三角形ABC中,若sin C = cos A + cos B,
求证三角形ABC为直角三角形.
sin C = cos A + cos B
2sin(C/2)cos(C/2)=2cos[(A+B)/2]cos[(A-B)/2]
∵cos[(A+B)/2]=sin(C/2)
∴cos(C/2)=cos[(A-B)/2]
0≤A,B,C≤180度
=> C=A-B
A+B+C=180度---(1)
A-B-C=0度-----(2)
(1)+(2),
A=90度
(其實B也可能是90度,關鍵在於cos A + cos B還是cos B + cos A而已,
這裡證得A=90度不失一般性吧^^...)
[ Last edited by 灰羊 on 6-12-2004 at 03:37 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 01:11 PM
|
显示全部楼层
发表于 3-12-2004 01:11 PM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
01/12/2004 星期三
初中(A45)
log_{2} 3 = a
3^{b} = 7
求 log_{12} 56
log_{2} 3 = a
=> 3=2^a
3^{b} = 7
=> 2^(ab)=7
log_{12} 56=㏒56/㏒12 (底數為2)
=㏒(7*2^3)/㏒(3*2^2)
=㏒ 2^(3+ab) / ㏒ 2^(2+a)
=(3+ab)/(2+a) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 01:11 PM
|
显示全部楼层
发表于 3-12-2004 01:11 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 01:25 PM
|
显示全部楼层
发表于 3-12-2004 01:25 PM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
02/12/2004 星期四
高中(A43)
60^{a} = 3 , 60^{b} = 5
求 12^{(1-a-b)/(2-2b)}
60^a=3
=> a=㏒_{60} 3
60^{b} = 5
=> b=㏒_{60} 5
(1-a-b)/(2-2b)=(1- ㏒_{60} 3 - ㏒_{60} 5)/2(1-㏒_{60} 5)
=(㏒_{60} 4)/2(㏒_{60} 12)
=(㏒_{12} 4)/2
=㏒_{12} 2
設12^{(1-a-b)/(2-2b)}=k,則
㏒_{12} k =(1-a-b)/(2-2b)
㏒_{12} k =㏒_{12} 2
=> k=2
即12^{(1-a-b)/(2-2b)}=2 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 3-12-2004 01:49 PM
|
显示全部楼层
灰羊 于 3-12-2004 01:11 PM 说 :
基本上換底公式是高一的課程...
是吗?
不好意思...我不是很清楚这些课程了.
 
不是form 3已经学习了吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 03:06 PM
|
显示全部楼层
发表于 3-12-2004 03:06 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 05:45 PM
|
显示全部楼层
发表于 3-12-2004 05:45 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 08:24 PM
|
显示全部楼层
发表于 3-12-2004 08:24 PM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
高中 (A37)
设 0<a,b<90度 , 且 sin a-sin b = -1/3
cos a - cos b= (2√2) /3
证明 b - a =60度
此題已有人解出
看一下吧^^ |
|
|
|
|
|
|
|
|
|
|
|
 发表于 3-12-2004 08:25 PM
|
显示全部楼层
发表于 3-12-2004 08:25 PM
|
显示全部楼层
多普勒效应 于 3-12-2004 15:06 说 :
指数与对数(包括换底等等)我们初三就学了...
...不愧是隆中華... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 10:24 PM
|
显示全部楼层
发表于 4-12-2004 10:24 PM
|
显示全部楼层
A , B是正整数,且A^2 + B^2 = 15
A^3 + B^3 = 28
问共有几组(A,B)
∵A , B是正整数,且A^2 + B^2 = 15
∴0<A^2<15
则A=1,2,3
(1)若A=1,则B^2 = 14,但B是正整数,故B不存在
(2)若A=2,则B^2 = 11,但B是正整数,故B不存在
(3)若A=3,则B^2 = 6,但B是正整数,故B不存在
故共有0组(A,B) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-12-2004 12:04 AM
|
显示全部楼层
发表于 6-12-2004 12:04 AM
|
显示全部楼层
小弟帮 Livar 兄贴的
C16:
Let A=1^n+2^n+3^n+4^n+5^n
Let == represent congruent mod 5
A == 1 +2^n + 3^n + 4^n
== 1 +2^n +(-2)^n + (-1)^n
== [ 1+(-1)^n ] [ 1+2^n ]
A is divisible by 5 is the RHS of the
congruent equation is zero.
(1)Case n=2l+1: where l=integer A is divisible by 5
n={1,3,5,7...}-->1002 solutions
(2)Case n=2l: then
A == 2[ 1+4^l ]
== 2[ 1+(-1)^l]
if l=2k+1 where is k is integer
then A is divisible by 5.
Hence n=4k+2 or n={2,6,10,14,18,...}-->501 solutions
Total up..there r 1503 solution |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 8-12-2004 09:06 PM
|
显示全部楼层
灰羊 于 3-12-2004 01:05 PM 说 :
sin C = cos A + cos B
2sin(C/2)cos(C/2)=2cos[(A+B)/2]cos[(A-B)/2]
∵cos[(A+B)/2]=sin(C/2)
∴cos(C/2)=cos[(A-B)/2]
0≤A,B,C≤180度
=> C=A-B
A+B+C=180度---(1)
A-B-C=0度-----(2)
(1) ...
对了.
灰羊 于 3-12-2004 01:11 PM 说 :
log_{2} 3 = a
=> 3=2^a
3^{b} = 7
=> 2^(ab)=7
log_{12} 56=㏒56/㏒12 (底數為2)
=㏒(7*2^3)/㏒(3*2^2)
=㏒ 2^(3+ab) / ㏒ 2^(2+a)
=(3+ab)/(2+a)
对
灰羊 于 3-12-2004 01:25 PM 说 :
60^a=3
=> a=㏒_{60} 3
60^{b} = 5
=> b=㏒_{60} 5
(1-a-b)/(2-2b)=(1- ㏒_{60} 3 - ㏒_{60} 5)/2(1-㏒_{60} 5)
=(㏒_{60} 4)/2(㏒_{60} 12)
=(㏒_{12} 4)/2
...
对
430201 于 4-12-2004 10:24 PM 说 :
A , B是正整数,且A^2 + B^2 = 15
A^3 + B^3 = 28
问共有几组(A,B)
∵A , B是正整数,且A^2 + B^2 = 15
∴0<A^2<15
则A=1,2,3
(1)若A=1,则B^2 = 14,但B是正整数,故B不存在
...
对了..该死.没有仔细看问题,竟然归类在高中.-_-
对不起,之前的分类一蹋糊涂.. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-12-2004 11:41 AM
|
显示全部楼层
发表于 9-12-2004 11:41 AM
|
显示全部楼层
06/12/2004 星期一
初中(A46)
考虑以下的步骤:
在无限多的步骤之后,我们可得
问,黑色格子的面积是整图案的百分之几?.
=================================================
這個的圖看不到 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-12-2004 11:48 AM
|
显示全部楼层
发表于 9-12-2004 11:48 AM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
07/12/2004 星期二
初中(A47)
写出以下算式:
* *
x * *
---------------
* * *
* * *
---------------
* * * *
+ 1 * *
---------------
* * * * *
---------------
*代表0到9中任何一个数字,不需是一样的.
就是写出每一个*代表什么数字.
應該只有一組解
9 9
x 9 9
---------------
8 9 1
8 9 1
---------------
9 8 0 1
+ 1 9 9
---------------
1 0 0 0 0
---------------
. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 9-12-2004 01:44 PM
|
显示全部楼层
灰羊 于 9-12-2004 11:41 AM 说 :
06/12/2004 星期一
初中(A46)
考虑以下的步骤:
在无限多的步骤之后,我们可得
问,黑色格子的面积是整图案的百分之几?.
=================================================
這個的圖看不到
看不到?..
这个,我想不到是什么问题呢!
我能够看得到啊! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-12-2004 03:47 PM
|
显示全部楼层
发表于 9-12-2004 03:47 PM
|
显示全部楼层
微中子 于 9-12-2004 13:44 说 :
看不到?..
这个,我想不到是什么问题呢!
我能够看得到啊!
http://tinypic.com/ 試試這裡?不用註冊的
我不知為甚麼看不到 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 9-12-2004 08:53 PM
|
显示全部楼层
多普勒效应 于 6-12-2004 12:04 AM 说 :
小弟帮 Livar 兄贴的
C16:
Let A=1^n+2^n+3^n+4^n+5^n
Let == represent congruent mod 5
A == 1 +2^n + 3^n + 4^n
== 1 +2^n +(-2)^n + (-1)^n
== [ 1+(-1)^n ] [ 1+2^n ]
A is divisible by 5 ...
对
灰羊 于 9-12-2004 11:41 AM 说 :
06/12/2004 星期一
初中(A46)
考虑以下的步骤:
在无限多的步骤之后,我们可得
问,黑色格子的面积是整图案的百分之几?.
=================================================
這個的圖看不到
明天我再看看.
灰羊 于 9-12-2004 11:48 AM 说 :
應該只有一組解
9 9
x 9 9
---------------
8 9 1
8 9 1
---------------
9 8 0 1
+ 1 9 9
---------------
1 0 0 0 0
---------------
.
对,可以解释吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-12-2004 05:22 PM
|
显示全部楼层
发表于 10-12-2004 05:22 PM
|
显示全部楼层
微中子 于 2-12-2004 22:11 说 :
09/12/2004 星期四
高中(B46)
找出所有domain是实数的涵数,符合:
1. f(1)=1
2. f(x_1 + x_2)=f(x_1)+f(x_2)
3. f(1/x) = 1/x^2 f(x), x不等于0.
(待解)
(答案:)
(解对者:)
∵f(a+b)=f(a)+f(b)
設f(x)=kx,
∵f(1)=1 => k=1
∴f(x)=x
代入3. f(1/x) = 1/x^2 f(x), x不等于0驗證,符合
∴f(x)=x
x屬於R
(不知這樣可不可以...) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-12-2004 05:28 PM
|
显示全部楼层
发表于 10-12-2004 05:28 PM
|
显示全部楼层
微中子 于 9-12-2004 20:53 说 :
对,可以解释吗?
好的
* * <=A
x * * <=B
---------------
* * *
* * *
---------------
* * * * <=C
+ 1 * * <=D
---------------
* * * * * <=E
---------------
∵E是5位數,D的最大值是199
∴C≧9801
而A*B的最大值為99*99=9801
∴A=B=99 => C=9801
∴D=199,E=10000
[ Last edited by 灰羊 on 10-12-2004 at 05:30 PM ] |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|