|
查看: 3063|回复: 22
|
请问ln和log有什么差别?
[复制链接]
|
|
|
 发表于 17-3-2008 11:59 PM
|
显示全部楼层
发表于 17-3-2008 11:59 PM
|
显示全部楼层
原帖由 liang_2002 于 17-3-2008 11:47 PM 发表 
请问ln和log有什么差别?
如题
log 一般上是base 10......而ln 是log base e (exponential) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-3-2008 11:39 PM
|
显示全部楼层
发表于 19-3-2008 11:39 PM
|
显示全部楼层
这两种对数在不同的领域上各有所长。
log 在一些分析和统计的书中直接就表示底为e 的对数;因为在那个领域以 e 为底是最方便的。
在化学课本中由于两种都用上,所以可能就会用log和ln 分别代表以10 或以e为底。也有人用lg代表以10 为底的对数。
符号是人规定的,没有对错;方便和流通性为主要考量。所以看书时应注意该书的符号。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-3-2008 11:35 AM
|
显示全部楼层
发表于 20-3-2008 11:35 AM
|
显示全部楼层
|
在我的context 里, log是 base 2 的。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 14-4-2008 09:48 PM
|
显示全部楼层
发表于 14-4-2008 09:48 PM
|
显示全部楼层
log是没有规定base什么的
如果log5就是log base 5
log7就是log base 7
lg 才是log base 10
ln (natural log)就是loge
e = 2.718281828...
这个constant很特别的
就是如果你拿到f(x) = e^x的微分
在x=0,其微分值等于1 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 15-4-2008 12:16 AM
|
显示全部楼层
发表于 15-4-2008 12:16 AM
|
显示全部楼层
回复 5# 無聊人 的帖子
好!
深入浅出!一看就明!  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 10:40 AM
|
显示全部楼层
发表于 16-4-2008 10:40 AM
|
显示全部楼层
在研究一个问题中,
我发现到e这个特别的数字从中跑了出来。
先问问大家一个有趣的问题。
假设你被判死刑,
在行刑前给你如下的选择:
① 10个枪手,准度皆为0.1。
② 100个枪手,准度皆为0.01。
③ 1000 个枪手,准度皆为0.001。
如果他们开枪后都没射中你,
则让你当众释放。
你会选择哪一组枪手对着你开枪呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 10:57 AM
|
显示全部楼层
发表于 16-4-2008 10:57 AM
|
显示全部楼层
回复 7# mathlim 的帖子
我选③  。。。。。。。。。。。。。。。。。。。。。。。 。。。。。。。。。。。。。。。。。。。。。。。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 01:59 PM
|
显示全部楼层
发表于 16-4-2008 01:59 PM
|
显示全部楼层
① 没被射中的概率 = 0.9^10 ≈ 0.3487
② 没被射中的概率 = 0.99^100 ≈ 0.3660
③ 没被射中的概率 = 0.999^1000 ≈ 0.3677
我选择③  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 03:45 PM
|
显示全部楼层
发表于 16-4-2008 03:45 PM
|
显示全部楼层
是的!
我们把情况两极化,
两个准度为1/2的对着你射,
是不是很可怕。
如果是一个准度为1的对着你射,
就必死无疑了!
如果是10000个准度为0.0001的对着你,
庞大的人数的确是吓人,
但是想一想,
说不好听,
是10000个拿着枪的大笨蛋。
那么n个准度为1/n的人射击,
n越大,射中率越小,
会一直小下去吗? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 07:35 PM
|
显示全部楼层
发表于 16-4-2008 07:35 PM
|
显示全部楼层
n个准度为1/n的人射击, 没有一个人射中我的概率是 (1-1/n)^n
graph 如下: 
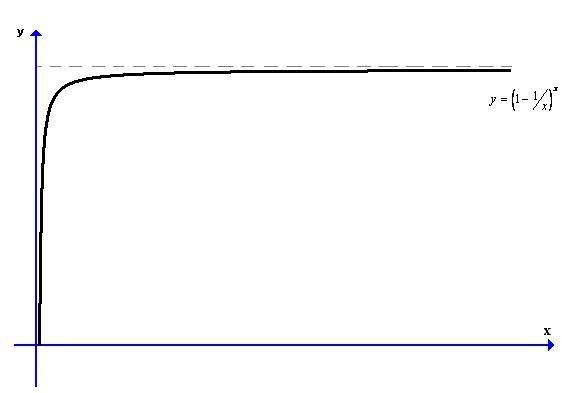 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-4-2008 11:16 PM
|
显示全部楼层
发表于 16-4-2008 11:16 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-4-2008 05:12 PM
|
显示全部楼层
发表于 17-4-2008 05:12 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-4-2008 06:43 PM
|
显示全部楼层
发表于 17-4-2008 06:43 PM
|
显示全部楼层
回复 13# 無聊人 的帖子
不是 1 
lim_{x → ∞} (1 - 1/x)^x ≈ 0.367879441 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-4-2008 08:54 AM
|
显示全部楼层
发表于 18-4-2008 08:54 AM
|
显示全部楼层
它的极限是 1/e ≈ 0.367879441... ...
欧拉数 e 跑出来了!  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-4-2008 05:50 PM
|
显示全部楼层
发表于 18-4-2008 05:50 PM
|
显示全部楼层
高二上微积分 Transcendental Functions 这一课的时候, 老师有教 e 这一个数的定义.
那时的定义是 : e = lim_{n → ∞} (1 + 1/n)^n .
我当时的问题就是: 为什么要这样定义它? 又为什么会这样定义它?  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-4-2008 01:05 PM
|
显示全部楼层
发表于 19-4-2008 01:05 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-4-2008 01:40 PM
|
显示全部楼层
发表于 19-4-2008 01:40 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-4-2008 01:48 PM
|
显示全部楼层
发表于 19-4-2008 01:48 PM
|
显示全部楼层
回复 18# flash 的帖子
那老师的回覆是: "人家这样定义就这样定义咯, 问酱多做什么? 你喜欢随便定义f,g,h 都可以, 看人家用不用而已.." 
这个答案让我觉得那个老师很不认真教学 =.= |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-4-2008 01:51 PM
|
显示全部楼层
发表于 19-4-2008 01:51 PM
|
显示全部楼层
回复 16# 多普勒效应 的帖子
对对对~我也想知道~ |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|