|
查看: 2744|回复: 15
|
F4 Add Maths - Quadratic Function
[复制链接]
|
|
|
参考书里的几个问题不会做,想请大家帮帮忙:
1. Find the range of value of x for which 2x^2-6x+5 lies between 1 and 25.
2. Find the range of values of m for which y=m(x^2-1) +4x+5 is always positive.
第二题我做到的答案是m>4,m<1,可是后面的答案是1<m<4 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 03:20 PM
|
显示全部楼层
发表于 16-5-2006 03:20 PM
|
显示全部楼层
原帖由 menglee 于 16-5-2006 02:55 PM 发表
参考书里的几个问题不会做,想请大家帮帮忙:
1. Find the range of value of x for which 2x^2-6x+5 lies between 1 and 25.
2. Find the range of values of m for which y=m(x^2-1) +4x+5 is always pos ...
1. 1 < 2x^2 - 6x + 5 < 25
2x^2 - 6x + 4 > 0
2(x-2)(x-1) > 0 -> x<1 ,x>2
2x^2 - 6x - 20 < 0
2(x-5)(x+2) < 0 -> -2<x<5
取两个range的intersection,得 -2<x<1 , 2<x<5
2.mx^2 + 4x + 5 - m >0 说明no solution for y = 0
用b^2 - 4ac < 0
16 - 4m(5-m) < 0
4m^2 - 20m + 16 < 0
4(m-1)(m-4) < 0
得 1<m<4.
[ 本帖最后由 hamilan911 于 16-5-2006 03:40 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 03:21 PM
|
显示全部楼层
发表于 16-5-2006 03:21 PM
|
显示全部楼层
1)2x^2-6x+5 lies between 1 and 25.
means 1=< 2x^2-6x+5<25
From 1< 2x^2-6x+5 ===> 2x^2-6x+4>0 --> 2(x-1)(x-2)>0
--> x>2 , x< 1 ...(i)
From 2x^2-6x+5<25 --> 2x^2-6x-20<0 -->2(x-5)(x+2)<0
--> -2< x < 5 ...(ii)
From (i),(ii) ,the range is -2<x<1 ; 2<x<5
2)y=m(x^2-1) +4x+5 is always positive.
means y=m(x^2-1) +4x+5>0
Consider three cases
(i) if m <0 , then it is n shape parabola , and it cannot be always >0
(ii)if m=0 then y=4x+5 which is also not always >0 ( example when x=-3)
(iii)if m>0 then since it is U shape parabola , y=mx^2+4x+5-m , using b^2-4ac <0
16-4m(5-m)<0 -->4m^2 -20m +16 < 0 --> 4(m-1)(m-4)<0
==> 1<m<4
哈哈,hamilan911 已经比我快一步了!
[ 本帖最后由 dunwan2tellu 于 16-5-2006 03:23 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-5-2006 04:32 PM
|
显示全部楼层
如果不画图表怎样可以直接知道4(m-1)(m-4)<0
==> 1<m<4。
还有4(m-1)(m-4)<0不可以直接simplify成(m-1)(m-4)<0吗?
--> x>2 , x< 1 ...(i)
--> -2< x < 5 ...(ii)
的intersection怎样知道?
[ 本帖最后由 menglee 于 16-5-2006 04:38 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 04:47 PM
|
显示全部楼层
发表于 16-5-2006 04:47 PM
|
显示全部楼层
原帖由 menglee 于 16-5-2006 04:32 PM 发表
如果不画图表怎样可以直接知道4(m-1)(m-4)<0
==> 1<m<4。
还有4(m-1)(m-4)<0不可以直接simplify成(m-1)(m-4)<0吗?
4(m-1)(m-4)<0是可以直接simplify成(m-1)(m-4)<0的。
你所谓的画图是garis nombor吗?其实不画图是可以知道range的。
ax^2 + bx + c = 0
若a > 0 ,graf会是U shape的。你可以想象一个U shape的graph,y=0的地方是x=m 和 x=n (m和n是它的root,m<n)
那么若y>0,则 x<m ,x>n
若y<0,则m<x<n.
若a < 0, ,graf会是反U shape的。你可以想象一个反U shape的graph,y=0的地方是x=m 和 x=n (m和n是它的root,m<n)
那么若y>0,则 m<x<n
若y<0,则x<m ,x>n.
但一般上考试都必须tunjuk langkah,所以你必须把他画出来,而且其他较复杂的function,你必须懂得graf如何画,才可以知道他的range.建议你保险起见,还是把他画出来比较安全。
这方法可以拿来double check answer.
至于intersection,你可以把garis nombor画出来,在原有的range上+ 和 - 的符号,就可以知道了。
dunwan2tellu ,你不是有mathematica吗?不如把garis nombor的一些技巧帖上来吧,比较容易看得清楚。
[ 本帖最后由 hamilan911 于 16-5-2006 04:51 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-5-2006 05:02 PM
|
显示全部楼层
|
还有,请问在画number line的时候怎样分向左还是右?谢谢 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 05:16 PM
|
显示全部楼层
发表于 16-5-2006 05:16 PM
|
显示全部楼层
原帖由 menglee 于 16-5-2006 05:02 PM 发表
还有,请问在画number line的时候怎样分向左还是右?谢谢
是指number line的箭头指向左右之类吗?
用例子解释会较清楚。
(x-1)(2-x) > 0
let x-1 >0 -> x>1
2-x >0 -> x<2
那么就画一条number line ,两点是1和2。
x>1 ,箭头指向右方,线上的符号是+,左方的“空白处”(没箭头的)符号是-
x<2 ,箭头指向左方,线上的符号也是+,右方的“空白处”符号是-
一般上我们都let例子中的 x-1和2+x 大过0,那么我们在画number line 时只需依照所找到的range画向左或向右(大过向右,小过向左),过后就一律在线上的符号放+ ,这样就不会搞混了。
而所要找的range就是要看这些符号相乘的结果了,如 ++得+, +-得-,-+得-,--得+。过后根据题目所求找出range,若<0就取-的部分,>0就取+的部分。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-5-2006 05:26 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 05:33 PM
|
显示全部楼层
发表于 16-5-2006 05:33 PM
|
显示全部楼层
其实作图很容易(最快的方法!)

这是那题 (m-1)(m-4)<0 的题目。颜色部分是你要的 range . |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 16-5-2006 05:36 PM
|
显示全部楼层
|
如果遇到没有intersect x-axis的case是不是就不能用画graph的方法呢? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 05:40 PM
|
显示全部楼层
发表于 16-5-2006 05:40 PM
|
显示全部楼层
原帖由 menglee 于 16-5-2006 05:36 PM 发表
如果遇到没有intersect x-axis的case是不是就不能用画graph的方法呢?
form 4 add math quadratic function 的题目,来来去去都是那几题,跑不掉的 。通常他们都会出 f(x)=(x-a)(x-b)的 pattern 的题目,所以大部分都能用 graph sketching 来做。 。通常他们都会出 f(x)=(x-a)(x-b)的 pattern 的题目,所以大部分都能用 graph sketching 来做。
如果没有 x-intersecting , 那么通常这类题目都和 b^2-4ac < 0 息息相关。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 16-5-2006 05:45 PM
|
显示全部楼层
发表于 16-5-2006 05:45 PM
|
显示全部楼层
原帖由 hamilan911 于 16-5-2006 04:47 PM 发表
4(m-1)(m-4)<0是可以直接simplify成(m-1)(m-4)<0的。
你所谓的画图是garis nombor吗?其实不画图是可以知道range的。
ax^2 + bx + c = 0
若a > 0 ,graf会是U shape的。你可以想象一个U shape的grap ...
霍米兰兄弟,我对 mathematica 还不够熟悉,就连刚刚的 graph 要农大也不会弄 。至于 number line 等我学会如何画先就可以post 上来了........ 。至于 number line 等我学会如何画先就可以post 上来了........ |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-5-2006 12:46 AM
|
显示全部楼层
发表于 18-5-2006 12:46 AM
|
显示全部楼层
原帖由 menglee 于 16-5-2006 02:55 PM 发表
参考书里的几个问题不会做,想请大家帮帮忙:
1. Find the range of value of x for which 2x^2-6x+5 lies between 1 and 25.
2. Find the range of values of m for which y=m(x^2-1) +4x+5 is always pos ...
这是我的做法,请参考:
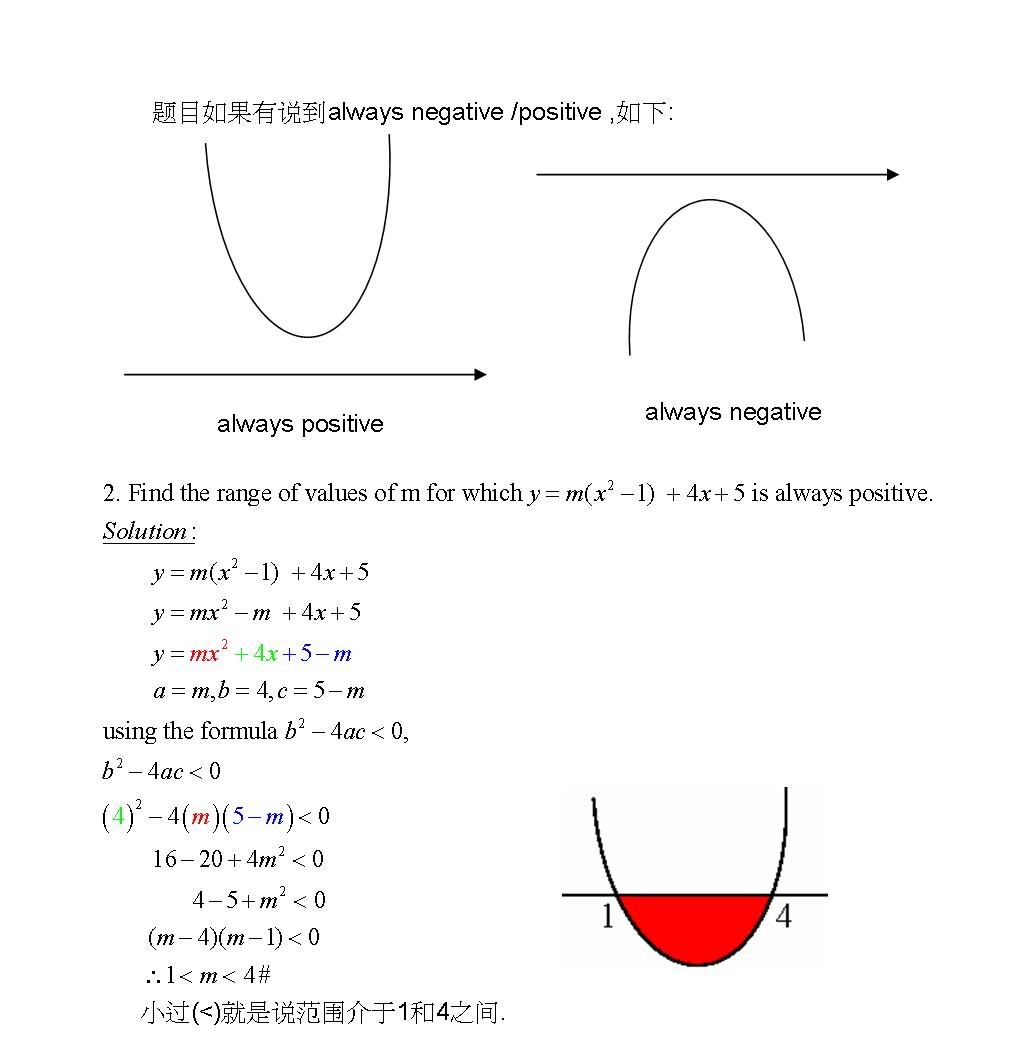
第一题我就不是很明白问法,因为我考SPM时是用BM的。
请问谁可以翻译成BM?
[ 本帖最后由 tayks88 于 18-5-2006 12:50 AM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-5-2006 11:31 AM
|
显示全部楼层
发表于 18-5-2006 11:31 AM
|
显示全部楼层
1. Find the range of value of x for which 2x^2-6x+5 lies between 1 and 25.
国语版:
Cari julat nilai bagi x supaya 2x^2-6x+5 sentiasa berada di antara 1 dan 25 . |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-5-2006 11:47 PM
|
显示全部楼层
发表于 18-5-2006 11:47 PM
|
显示全部楼层
原帖由 tayks88 于 18-5-2006 12:46 AM 发表
这是我的做法,请参考:

第一题我就不是很明白问法,因为我考SPM时是用BM的 ...
漏了m --> - 5m
其实,如果问题问得比较难些
你就真的要看清楚了
有些values是必须reject的
到了更高程度,你会发现到,画curve来找range of values是不够的 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-5-2006 12:04 AM
|
显示全部楼层
发表于 19-5-2006 12:04 AM
|
显示全部楼层
原帖由 無聊人 于 18-5-2006 11:47 PM 发表
漏了m --> - 5m
其实,如果问题问得比较难些
你就真的要看清楚了
有些values是必须reject的
到了更高程度,你会发现到,画curve来找range of values是不够的
谢谢你的宝贵意见。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|