|
查看: 1708|回复: 6
|
Geometry(form6)
[复制链接]
|
|
|
想请教各位这几题数学题如何解:
1.In triangles ABC,AB=AC;BC is produced to any point K,and AK is joined.If a triangle is drawn in which 2 of the angles are equal to <CAK,<BAK,respectively,prove that the thrid angle is equal to 2<CKA
2.ABC is an acute angleed triangle;ABP,ACQ are equilateral triangles outside ABC.Prove that triangle PAC=triangle BAQ
.If CP cuts BQ at R,prove that<BRC=120
3.Y is any point on the side BC of the equilateral triangle ABC;BYKis an equilateral triangle outside triangleABC, prove that AY=KC;<BAY=<KCY;<YAC=<YKC |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 29-1-2005 11:21 AM
|
显示全部楼层
GEOMETRY THEOREM
|
谁可geometry thereom(中六)的,最好是华语解释的,因为课本上的我看不懂。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-1-2005 11:32 PM
|
显示全部楼层
发表于 29-1-2005 11:32 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 7-2-2005 05:26 PM
|
显示全部楼层
蝎杰 于 6-1-2005 02:58 PM 说 :
想请教各位这几题数学题如何解:
1.In triangles ABC,AB=AC;BC is produced to any point K,and AK is joined.If a triangle is drawn in which 2 of the angles are equal to <CAK,<BAK,respectively,pr ...
1.在三角形ABC,AB=BC。BC延长至K点,之后与A连接成为AK。如果三角形里任何两个角度=<CAK,<BAC。请证明第三个角度=2<CRA。
2.ABC是个有锐度的三角形。而ABP,ACQ是ABC外面的等边三角形。请证明PAC=BAQ
如果CP穿过BQ至R点,请证明:<BRC=120
3.ABC是个等边三角形。Y则是BC的某一点,BYK是ABC外面的等边三角形。请证明:AY=KC,<BAY=<KCY,<YAC=<YKC |
|
|
|
|
|
|
|
|
|
|
|
 发表于 12-2-2005 06:55 PM
|
显示全部楼层
发表于 12-2-2005 06:55 PM
|
显示全部楼层
蝎杰,你的翻译有一些问题害我檬查查。
关于第一题。
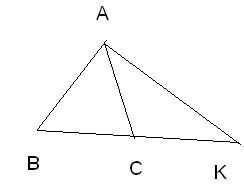
从题目我们可知,可假设一个三角形。三角分别是∠CAK,∠BAK 和2∠CKA, 三角相加等于180。
因此只要证明∠CAK,∠BAK 和2∠CKA=180 就破题。
∠ABK+ ∠BKA+∠KAB=180(given)
∠ABK=∠ACB(等腰三角形)
∠ACB+∠BKA+∠KAB=180
∠ACB=∠CAK+∠CKA(the sum of the interiior ∠=exterior ∠,忘了,应该是这样)
∠CAK+∠CKA+∠BKA+∠KAB=180
∠CAK+∠CKA+∠CKA+∠BAK=180
2∠CKA+∠CAK+∠BAK=180(sum of the interior angle of triangle)
hence, 若∠CAK,∠BAK是三角形的两个角,第三个角则是2∠CKA。
呵呵,第一次来这个论坛,其他两个待会儿。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-2-2005 08:50 AM
|
显示全部楼层
发表于 13-2-2005 08:50 AM
|
显示全部楼层
蝎杰 于 6-1-2005 02:58 PM 说 :
想请教各位这几题数学题如何解:
1.In triangles ABC,AB=AC;BC is produced to any point K,and AK is joined.If a triangle is drawn in which 2 of the angles are equal to <CAK,<BAK,respectively,pr ...
Q1 翻译好像有点问题。 看到我blur blur。 搂主纠正一下吧。
2。 ABP,ACQ是ABC外面的等边三角形,
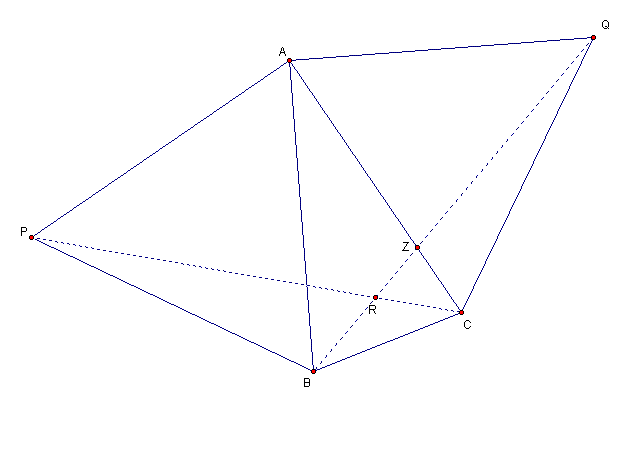
PAC = PAB + BAC;
BAQ = QAC + CAB;
ABP,ACQ = 等边三角形;
PAB = QAC = 60, BAC = CAB.
所以, PAC = BAQ.
PA = AB; AC=AQ; 角PAC =角 BAQ.
所以, 三角形PAC = 三角形BAQ.
角ACP = 角AQB.
再看 三角形AZQ 和 三角形ZRC.
角AQZ = 角 ZCR; 角AZQ = 角 RZC. 所以, 角ZRC = 角 QAZ = 60
BRC 就等于 180-60 = 120。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 13-2-2005 09:10 AM
|
显示全部楼层
发表于 13-2-2005 09:10 AM
|
显示全部楼层
Q3:
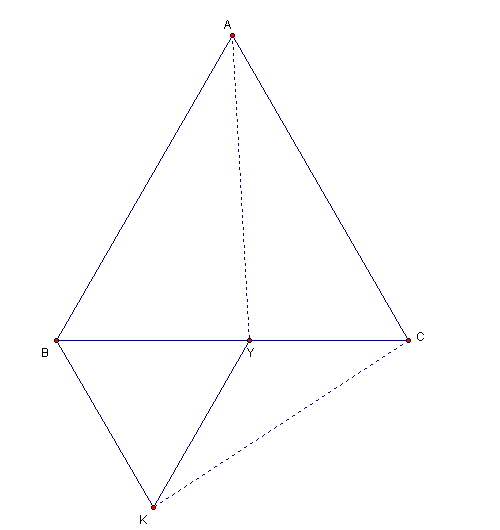
BK = BY; BC = BA; 角YBK = 角YBA
YA = sqrt (AB^2 + BY^2 - 2.AB.BY.cos ∠60)
= sqrt (BC^2 + BK^2 - 2.BC.BK.cos ∠60)
= KC.
已证 YA = KC, 用 sin(a)/a = sin(b)/b = sin(c)/c 就可以证明∠BAY=∠KCY,∠YAC=∠YKC |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|