|
|
 发表于 9-6-2004 07:43 PM
|
显示全部楼层
发表于 9-6-2004 07:43 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 9-6-2004 07:58 PM
|
显示全部楼层
发表于 9-6-2004 07:58 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-6-2004 12:48 AM
|
显示全部楼层
发表于 10-6-2004 12:48 AM
|
显示全部楼层
我試試
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-6-2004 07:50 AM
|
显示全部楼层
多谢 sinchee 的指正。。。
我已修改了当中的错误。再次谢过。。。
sinchee 于 9-6-2004 06:31 PM 说 :
sin(Π/5)[cos(2Π/5) + cos(4Π/5)] = sin(Π/5) [2cos(3Π/5)cos(Π/5)]
= cos(3Π/5)sin(2 ...
这个方法不错!
情~風 于 10-6-2004 12:48 AM :

情~風 的方法一次过解了我的两个问题。。。
佩服!佩服。。。
[ Last edited by pipi on 18-6-2004 at 11:14 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-6-2004 08:40 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 10-6-2004 09:20 AM
|
显示全部楼层
sinchee 于 9-6-2004 06:31 PM 说 :
sin(Π/5)[cos(2Π/5) + cos(4Π/5)] = sin(Π/5) [2cos(3Π/5)cos(Π/5)]
= cos(3Π/5)sin(2 ...
以 sinchee 的解法,我们又可以将问题一般化。
试试以下问题:

[ Last edited by pipi on 11-6-2004 at 03:54 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-6-2004 11:29 AM
|
显示全部楼层
sinchee 提议比 "楼上(i)" 更加一般化的题目。如下:
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 27-6-2004 10:47 PM
|
显示全部楼层
发表于 27-6-2004 10:47 PM
|
显示全部楼层
pipi 于 6-6-2004 12:51 说 :
现在,试试这题;
证明:(当然不可用计算机)

(多普勒效应 曾经在"数学挑战!"
强 曾经在"奥林比克" 及"难题" 问过 ...
我的解答

[ Last edited by wenshan on 29-6-2004 at 01:42 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 22-7-2004 08:07 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-10-2004 12:49 PM
|
显示全部楼层
发表于 20-10-2004 12:49 PM
|
显示全部楼层
7(i) 懒惰的方法 :-P
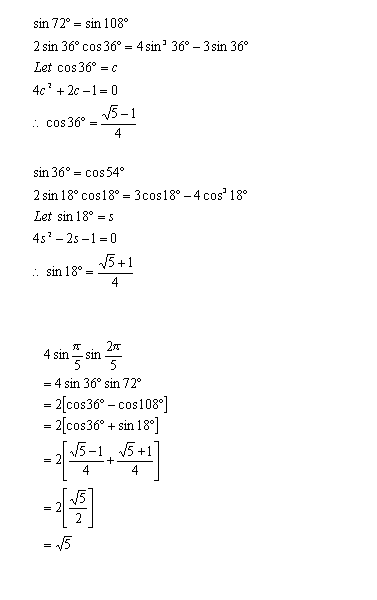 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-10-2004 01:35 PM
|
显示全部楼层
发表于 20-10-2004 01:35 PM
|
显示全部楼层
这题看来可以推广。。。
2^n * sin[ pi/(2n+1) ] * sin [2pi / (2n+1)] * ... * sin [npi / (2n+1)] = sqrt(2n+1)
证了这个,就解决了这类的特别例子。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-11-2004 01:22 PM
|
显示全部楼层
发表于 6-11-2004 01:22 PM
|
显示全部楼层
pipi 于 2-6-2004 12:42 PM 说 :
3.

不用sin18,可用構造對偶法
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-11-2004 07:32 PM
|
显示全部楼层
发表于 6-11-2004 07:32 PM
|
显示全部楼层

別人幫解的
(1)∵x^(2n+1)=1之2n+1個根為coskθ+isinkθ,k=0,1,2,...2n
∴由根與係數知:1+(cosθ+isinθ)+(cos2θ+isin2θ)+...+(cos2nθ+isin2nθ)=0
=>1+cosθ+cos2θ+...+cos2nθ=0.......(a)
∵cos(n+1)θ=cos(2n+2)π/2n+1=cos[2π-(2nπ/2n+1)]=cos2nπ/2n+1=cosnθ
同理:cos(n+2)θ=cos(n-1)θ,...,cos2nθ=cosθ,代入(a)式可得
=>1+2[cosθ+cos2θ+...+cosnθ]=0
∴cosθ+cos2θ+...+cosnθ=-1/2
====================================================================
(2)設S=coskθ+cos2kθ+...+cosnkθ
=>2sin(kθ/2)S=2sin(kθ/2)coskθ+2sin(kθ/2)cos2kθ+...+2sin(kθ/2)cosnkθ
=[sin(3kθ/2)-sin(kθ/2)]+[sin(5kθ/2)-sin(3kθ/2)]+...
[sin(2n+1)kθ/2-sin(2n-1)kθ/2]
=sin(2n+1)kθ/2-sin(kθ/2)
=2cos(n+1)kθ/2sin(nkθ/2),將θ=2nπ/2n+1代入
=2cos[kπ-(nkπ/2n+1)]sin(nkπ/2n+1)
=(-1)^k×2cos(nkπ/2n+1)sin(nkπ/2n+1)
=(-1)^k×sin(2nkπ/2n+1)
=(-1)^k×sin[kπ-(kπ/2n+1)]
=(-1)^k(-1)^(k+1)×sin[kπ-(kπ/2n+1)]
=-sin(kπ/2n+1)=-sin(kθ/2)
∴S=-1/2
故coskθ+cos2kθ+...+cosnkθ=-1/2 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|