什么是四维空间？？

rEborN12

0维空间＝一点。。
一维空间＝一线（长）。。
二维空间＝长x宽。。＝平面。。＝2D。。
三维空间＝长x宽x高。。＝立体。。＝3D。。

那么四维空间＝？？
我听过四维空间＝长x宽x高x时间。。
是吗？？
有谁听过？？

[ 本帖最后由 rEborN12 于 4-7-2007 02:49 AM 编辑 ]

rEborN12

在其他帖看到了这个。。

原帖由 我是元元~ 于 11-3-2007 01:22 PM 发表
四维空间 - 除了 高、长、宽，即我们一般了解的xyz铀，还有一个，叫做时间铀。高长宽的空间 加上 时间铀， 就是时空。

如果我们了解要如何在时间铀上随意移动，那么，来回过去现在未来，就会和来回马来西亚星加坡泰国那样简单。

然而，
在时间铀上不规则地移动而发生的事件是在我们的理解之外，
一个人前往以前的时空时做出了什么事，往往会对多个相应的时空产生影响。
这个因为突破了四维空间的常理（如时光逆流）而产生“ 蝴蝶效应”
则是一个活在四维空间但只是理解三维事物的我们难以想象的现象，一如活在二维世界的扁片人不能理解 “高” 是怎么一回事那样。

很赞同蝴蝶效应的说法。。
任何在时间穿梭里造成的一丝变动或更改。。
都会是引起未来改变的关键。。

另。。蚂蚁就活在二维空间。。
它们的世界就只有平面。。

[ 本帖最后由 rEborN12 于 26-6-2007 12:33 AM 编辑 ]

神经质女王

什么是蝴蝶效应/？？？

GeR

原帖由 rEborN12 于 25-6-2007 03:11 AM 发表
一维空间＝一点。。
二维空间＝长x宽。。＝平面。。＝2D。。
三维空间＝长x宽x高。。＝立体。。＝3D。。

那么四维空间＝？？
我听过四维空间＝长x宽x高x时间。。
是吗？？
有谁听过？？

一点 不是一维空间吧！！！

rEborN12

四维空间

四维空间是一个时空的概念。简单来说，任何具有四维的空间都可以被称为“四维空间”。不过，日常生活所提及的“四维空间”，大多数都是指爱因斯坦在他的《广义相对论》和《狭义相对论》中提及的“四维时空”概念。根据爱因斯坦的概念，我们的宇宙是由时间和空间构成。时空的关系，是在空间的架构上比普通三维空间的长、宽、高三条轴外又加了一条时间轴，而这条时间的轴是一条虚数值的轴。 根据爱因斯坦相对论所说：我们生活中所面对的三维空间加上时间构成所谓四维空间。由于我们在地球上所感觉到的时间很慢，所以不会明显的感觉到四维空间的存在，但一旦登上宇宙飞船或到达宇宙之中，使本身所在参照系的速度开始变快或开始接近光速时，我们能对比的找到时间的变化。如果你在时速接近光速的飞船里航行，你的生命会比在地球上的人要长很多。这里有一种势场所在，物质的能量会随着速度的改变而改变。所以时间的变化及对比是以物质的速度为参照系的。这就是时间为什么是四维空间的要素之一。 什么是四维？现在的说法是三维空间加上时间这一维，构成所谓的四维空间。然而，这种说法是一击即破的。为什么？我们可以从二维来考虑。 一个二维生物（如果有的话），他们考虑所谓的三维空间绝对和我们的三维空间不同——他们会把时间作为第三维，因为他们无法感受这一维的存在。 同样，我们现在也走进了这个误区，把时间算做第三维。可能四维生物看到我们在宣扬这种思想时，也在为我们叹息。 那么时间算不算一维？在我看来，时间应该是一维，即在多维生物本身的维度之外再加一维，构成新的N+1维空间，而且这样也有助于帮我们解决一些问题，也可以使我们对比三维维度更高的空间加深认识。 我有一个更新的构想，即所有的维度都是由时间构成，没有时间，就没有空间，包括最基本的一维空间。这应该好理解，因为没有时间，空间本身的存在就没有任何意义，因为时空本身就是不能分割的整体。那么，为什么一种时间可以形成不同的维度空间？这里，我们可以把时间看成是一种可以分解的常量。 时间可以分解，这一句话理解起来可能有点困难。但是，只要想通了道理也是很简单的。要明白这个道理，首先必须了解两点。 第一是时空的不可分性，这一点估计大家都明白，离开了空间谈时间，或者离开了时间谈空间，都是毫无意义的。 第二点是时间的多样性，这一点了解起来可能有一点麻烦。在日常生活中，我们接触到的都是时间的合成体，也就是各个分时间有机结合形成的一个总的时间体系。可能你们会觉得我是在狡辩，其实不是。只要你们换一个角度去想，一个结果，可能是几个不同的原因形成的。就拿运动来说，我们观察到的一般都是几个不同运动产生的一种运动的结合体，即合运动。 关于时间，我们也可以这样去想。我们看到的时间结合体，可以是由物体运动的时间，历史时间（即经历时间）和其他的一些时间构成。而运动时间，我们又可以看成由上下运动的时间，左右运动的时间和前后运动的时间。当然，划分方法是多样的，这就构成了时间的多样性，至于如何去划分，这就要由不同的情况而定。 一部分时间对应一段空间。在这个不完整的空间里，时间起到了决定性的作用。我们之所以是三维生物，是以为这个维度的空间里只存在三维的时间。 时间的不完整决定了空间的不完整。我们不能认识其他维度的空间，是因为我们不具备在那个空间里面运动的时间。时间的多样性决定的空间的多样性。 同时，因为时间的不同分解方式，注定了我们的三维空间也是相对的，它可以被命名为一维，二维，甚至是任意维——完全取决于不同的分解方式。 时间是决定维度的关键，同时，它也是决定低维物体高维存在方式的关键。 在谈论我的看法之前，先让我们看看科学上的说法：低维是空间上读缺陷，它们不具备在高维世界内运动的空间。关于这一点，我有一个疑问，那就是我们怎么可以发现这个缺陷。我们认为的低维不存在某一个空间长度，是因为我们无法确定它有那一个长度，也就是我们现在用最好的设备也无法观察到那一个长度差。那么，将来呢？ 我们现在无法认证，可能将来会有人证明那个低维物体确实属于高维。因此，低维与高维并不存在所谓的空间差。那么，我们如何区别高维与低维？很简单，用时间。 用时间去解释任何一个纬度空间，我们也可以认为，低维之所以比高维低级，是因为它们存在时间上的缺陷，它们无法在时间范畴内感受高维的存在。所以，我们要去了解低维或者高维，先要知道它们存在的时间范围。 高维与低维之间可以实现转化，道理是很简单的，只要加入或者去掉一个时间单位就可以了。然而说起来很容易，做起来却很复杂，我们对时间的概念都是如此模糊，要想在空间范围类实现时间的转化就更困难。 对四维空间，一般人可能只是认为在长、宽、高的轴上，再加上一根时间轴，但对于其具体情况，大部分的人仍知之甚少。 有一位专家曾打过一个比方：让我们先假设一些生活在二维空间的扁片人，他们只有平面概念。假如要将一个二维扁片人关起来，只消用线在他四周画一个圈即可，这样一来，在二维空间的范围内，他无论如何也走不出这个圈。 现在我们这些生活在三维空间的人对其进行“干涉”。我们只需从第三个方向（即从表示高度的那跟轴的方向），将二维人从圈中取出，再放回二维空间的其他地方即可。 对我们这些三维人而言，四维空间的情况就与上述解释十分类似。如果我们能克服四维空间，那么，在瞬间跨越三维空间的距离也不是不可能。 相关资料，也是规律论对四维空间的认识！ 四维空间对人类来说不过是部电影  对于多维空间我不想说什么，我现在只讲四维空间！在科学界，四维空间被认为是时间轴与三维空间的结合，并提出可以通过时间轴看到过去与未来——在这我本来有话要说，但为了文字通顺我还是放到后面来讲——但一些学者把四维空间和黑洞联系起来认为四维空间可以让我们回到过去或进入未来。 在我讲过去与未来时我先讲一下世界的唯一性，现在的宇宙学和天体学之类的都承认了暗物质和暗能量，并提出了多宇宙这一概念。而我要说的是我们这个宇宙，而不是多宇宙中相似的宇宙。在指明我们现存唯一性的宇宙时，我们来讲我们的过去与未来，在此我先不讲四维空间（也就是时间轴这一概念）是否能把我们带到过去或未来。我要讲的是当我过回到过去或进入未来，当那促行为成为现实时，那他所处于宇宙还是我们的吗？  第一：回到过去，那么他们的历史还是我们现在的历史吗？他们的行为会对历史产行作用吗？如果产生作用，那么他们的历史就不是我们今天的历史，如果不能产行作用，那么作们的行为是真正的回到过去了吗？ 从另一个角度来说，也就是说他们回到过去之后有实质的躯体和质量吗？如果有那么历史改变那是尽然的。如果没有那么他们的行为就不成构成回到过去——我再来强调一次如果真能回到过去那么，它只能用多宇宙这一说法讲，那就是回到了一个类史的过去，他将不能成为我们现在的过去。  我们现在来讲进入未来，如果可以通过时间轴进入未来。那么未来还是未来吗？在这我不是用咬文嚼字这一方式来辩正在它是不是我们的未来，我要说的是如果进入了未来——为了更简单的说明我们就不说进入了未来，就说是看到了未来——那么那未来还会一模一样的发展下去吗？你如你看到在两日后自己因一事遇上了灾难,那你还能让那事完全重演吗？就算能达到完全重演，那在过程中你的心态还是你两天前看到的吗？如果一个谎言在三天后被人类识破，那么在四天前就有人看到了（知道了）那么这一行为还能成立吗——在这么多决定性因素当中有一个改变了，那么那个宇宙或世界还能是我们的吗？     这样看来，我们的宇宙或世界是以这切不变的形式下成立的，那么四维空间对我们来说难道不是一部电影吗？（当然说这名话的口气是在已否定四维空间可以把我们带到过去或进入未来）     人们现在再来看一下四维空间是否能把我们带到过去或未来，零维空间被定意为点 ，一维空间被定意为长（点组成的），二维空间被定意为宽（长和宽组成的）——也就是平面，我只是用土话给大家讲这样好理解，但不要误解——,三维空间被定意为立体空间（也就是所谓的静态的空间），在三维的基础上加了时间轴就是所谓的四维空间，现在的科学还是以认识到的为准。我一直在考虑时间该不该排在第四，在现实中还有很多不被承认现实，这些都是暗物质和暗能量中九牛一毛都谈不上的实体！

rEborN12

The fourth spatial dimension and orthogonalityA right angle is defined as one quarter of a revolution and "orthogonal" (from the Greek) refers to co-ordinates or functions that are at right angles to each other. Cartesian geometry arbitrarily chooses orthogonal directions through space, which means that they add height. The fourth dimension is therefore the direction in space that is at right angles to these three observable directions.

Vectors[url=http://en.wikipedia.org/wiki/Imageice_analogy-_1_to_5_dimensions.svg][/url] [url=http://en.wikipedia.org/wiki/Imageice_analogy-_1_to_5_dimensions.svg][/url]
Demonstration of objects with 1 to 5 dimensions


‎
The fourth spatial dimension can be thought of in terms of vectors, analogous to arrows, fixed from some single place in space which we call the origin, that point to other places. These are called geometric vectors.
A point is a zero-dimensional object. It has no extension in space, and no properties. If one were to think of this point as a geometric vector, like an arrow, it would have no length. This vector is called the zero vector.
A line is a one-dimensional object. If we pick some nonzero vector in some direction, this vector has some definite length. That vector has a head at some point in space and a tail at the origin. If we think of stretching that vector so it is twice as long, three times as long, and so on and even stretching it backwards so it takes all possible lengths it can (even zero length, to get the zero vector), we get a single line with one dimension of length. All the vectors that describe points on this line are said to be parallel to each other. Even though any line we can draw must have some small thickness (so that we can see it), this theoretical line does not.
A plane is a two-dimensional object. It has a finite length and breadth but no thickness — somewhat like a sheet of paper (but paper too has some thickness). Thinking of a plane in terms of vectors can be a little more challenging. If we think of taking one vector and moving it so that its tail is touching the head of the first and forming a vector with its tail at the origin and the head at the head of the repositioned second vector, we have a reasonable way of talking about adding vectors. If we have two vectors that are not parallel, we can talk about all the points we can reach by stretching either of the vectors (or not stretching them), and, adding these vectors together, these points form a plane. We say that the two vectors span the plane.
Space, as we perceive it, is three-dimensional. We can think of putting a line together with a "stack" of planes. These planes are "stuck together" like a sandwich, with the line passing through them like a skewer. To get to some point in space, we can imagine traveling up the line and then moving across the plane to the point. We then have three vectors to think about, one to travel some distance up the line and two to get to some point in space.
The fourth spatial dimension, then, can be described by "sticking together" several three-dimensional spaces in a row. To get to some point in the four-dimensional space, one travels along the three-dimensional spaces, and also across the fourth dimension. The total number of vectors involved is four.
Mathematically, the 4-dimensional spatial equivalent of conventional 3-dimensional geometry is the Euclidean 4-space, a 4-dimensional normed vector space with the Euclidean norm. The "length" of a vector
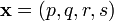expressed in the standard basis is given by
which is the natural generalisation of the Pythagorean Theorem to 4 dimensions. This allows for the definition of the angle between two vectors (see Euclidean space for more information).

Geometry with four spatial dimensions
A 3D projection of a rotating 24-cell. It rotates simultaneously about two orthogonal planes.


In four spatial dimensions, Euclidean geometry provides for a greater variety of shapes to exist than in three dimensions. Just as three-dimensional polyhedrons are spatial enclosures made out of connected two-dimensional faces, the four-dimensional polychorons are enclosures of four-dimensional space made out of three-dimensional cells. Where in three dimensions there are exactly five regular polyhedrons, or Platonic solids, that can exist, six regular polychorons exist in four dimensions. Five of the six can be interpreted as natural extensions of the Platonic solids, just as the cube, itself a Platonic solid, is a natural extension of the two-dimensional square.
The pentachoron is constructed out of 5 tetrahedrons for cells and 10 triangular faces, and is the four-dimensional analogue of the tetrahedron. The tesseract is made out of 8 cubic cells and 24 squares, and is the four-dimensional hypercube. The tesseract's dual, the 16-cell, is the equivalent of the octahedron, as they are both cross-polytopes.
The 120-cell and 600-cell are duals of each other, and are analogous to the dodecahedron and icosahedron, respectively. The 24-cell is the unique regular polychoron in that it has no three-dimensional equivalent.
There are also a large set of semiregular polychora, called convex uniform polychoron, most of which can be derived from the 6 regular forms above.
Just as the sphere, or 2-sphere, is a curved two-dimensional surface made up of all points equidistant from a given central point in three-dimensional space, the 3-sphere, a kind of hypersphere, is the space containing all points equidistant to a given central point in four-dimensional space. Every three-dimensional cross section of a 3-sphere is a 2-sphere.

rEborN12

Dimensional analogy
A net of a tesseract


To make the leap from three spatial dimensions into four, a device called dimensional analogy is commonly employed. Dimensional analogy is studying how (n – 1) dimensions relate to n dimensions, and then inferring how n dimensions would relate to (n + 1) dimensions.
For example, in Edwin Abbott Abbott's book Flatland, he writes about a square that lives in a two-dimensional world, like the surface of a piece of paper. A three-dimensional being has seemingly god-like powers from the perspective of this square: such as being able to remove objects from a safe without breaking it open (by moving them across the third dimension), see everything that from the two-dimensional perspective is enclosed behind walls, and remaining completely invisible by standing a few inches away in the third dimension. By applying dimensional analogy, one can infer that a four-dimensional being would be capable of similar feats from our three-dimensional perspective. Rudy Rucker demonstrates this in his novel Spaceland, in which the protagonist encounters four-dimensional beings who demonstrate such powers.
A useful application of dimensional analogy in visualizing the fourth dimension is in projection. A projection is a way for representing an n-dimensional object in n − 1 dimensions. For instance, computer screens are two-dimensional, and all the photographs of three-dimensional people, places and things are represented in two dimensions by removing information about the third dimension. In this case, depth is removed and replaced with indirect information. The retina of the eye is a two-dimensional array of receptors but it can allow the brain to perceive the nature of three-dimensional objects using indirect information (such as shading, foreshortening, binocular vision etc.). Artists use perspective to give three-dimensional depth to two-dimensional pictures.
Similarly, objects in the fourth dimension can be mathematically projected to the familiar 3 dimensions, where they can then be more conveniently examined. In this case, the 'retina' of the four-dimensional eye is a three-dimensional array of receptors. A hypothetical being with such an eye would perceive the nature of four-dimensional objects using indirect information contained in the images it receives in its retina. Perspective projection from four dimensions produces similar effects as in the three-dimensional case, such as foreshortening. This adds four-dimensional depth to these three-dimensional pictures.
Dimensional analogy also helps in understanding such projections. For example, two-dimensional objects are bounded by one-dimensional boundaries: a square is bounded by four edges. Three-dimensional objects are bounded by two-dimensional surfaces: a cube is bounded by 6 squares. By applying dimensional analogy, one may infer that a four-dimensional cube, known as a tesseract, is bounded by three-dimensional volumes. And indeed, this is the case mathematically: the tesseract is bounded by 8 cubes. Knowing this is key to understanding how to interpret a three-dimensional projection of the tesseract. The boundaries of the tesseract project to volumes in the image, not merely two-dimensional surfaces. This helps in understanding features of such projections that may otherwise be very puzzling.
Likewise the concept of shadows can help us better understand the theory of four dimensions. If you were to shine a light on three dimensional object, it would cast a two dimensional shadow. Therefore light on a two-dimensional object would cast a one-dimensional shadow (in a two-dimensional world), and light on a one-dimensional object in a one-dimensional world would cast a zero-dimensional shadow, that is, a point of non-light. This idea can be used in the other direction; light on a four-dimensional object would cast a three-dimensional shadow.
As an example of this, imagine that light is shone down through a wireframe cube onto a flat surface. The shadow that results is that of a square within a square with each of the corners connected. Similarly, if a four-dimensional cube were lit "from above", its shadow would be that of a three-dimensional cube within another three-dimensional cube.
Being three-dimensional we are only able to see the world with our eyes in two dimensions; a four-dimensional being would see the world in three. Thus it would be able, for example, to see all six sides of an opaque box simultaneously. Not only so; it would also be able to see what was inside the box at the same time, just like in Flatland, where the sphere sees objects in the two-dimensional world and everything inside them simultaneously. Analogously, a four-dimensional viewer would see all points in our 3-dimensional space simultaneously, including the inner structure of solid objects and things obscured from our three-dimensional viewpoint.
Reasoning by analogy from familiar lower dimensions can be an excellent intuitive guide, but care must be exercised not to accept results that are not more rigorously tested. For example, consider the formulas for the circumference of a circle C = 2πr and the surface area of a sphere: A = 4πr2. One might be tempted to suppose that the surface volume of a hypersphere is V = 6πr3, or perhaps V = 8πr3, but either of these would be wrong. The correct formula is V = 2π2r3.

rEborN12

这是找到的一点资料。。
本身还没消化。。
不好意思。。

rEborN12

原帖由 GeR 于 3-7-2007 09:56 PM 发表


一点 不是一维空间吧！！！

怎么说呢？？

rEborN12

原帖由 神经质女王 于 1-7-2007 05:28 PM 发表
什么是蝴蝶效应/？？？

其大意为：一只南美洲亚马孙河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可能在两周后引起美国德克萨斯引起一场龙卷风。其原因在于：蝴蝶翅膀的运动，导致其身边的空气系统发生变化，并引起微弱气流的产生，而微弱气流的产生又会引起它四周空气或其他系统产生相应的变化，由此引起连锁反映，最终导致其他系统的极大变化。

此效应说明，事物发展的结果，对初始条件具有极为敏感的依赖性，初始条件的极小偏差，将会引起结果的极大差异。

对！
你没提起也没人注意到。

0D - a dot
1D - a line
2D - a flat surface
3D - an object (space)
4D - space-time
.
.
.
.
10 / 11D - ... ...

读了一本著名的书说，我们活着的宇宙其实是多维的。（共高达10或11维）
这些其他的为存在着只是我们无法体会到而已。

rEborN12

是吗？？
一直以为最基本是从1d开始的。。
因为一条线是从很多点组成的。。
所以就算再细。。
也有它的宽（长是肯定有了）。。
所以是宽x长。。
属于2d。。
不是酱吗？？

原帖由 'e-liang' 于 4-7-2007 02:06 AM 发表

读了一本著名的书说，我们活着的宇宙其实 ...

这个帖7也有提到。。
就好像蚂蚁永远不知道自己是活在3维空间。。

其实4维空间也未必是3维空间x时间。。
只知道时间是其中一维空间。。
就当作N维空间。。
N＝未知数x时间。。

rEborN12

不好意思。。
推翻了自己刚才所说的。。

这里又找到了一些资料。。

多维空间

“维”是一种度量，在三维空间坐标上，加上时间，时空互相联系，就构成四维时空。现在科学家的理论认为整个宇宙是十一维的，只是人类的理解只能理解到３维，打个比喻：一个智能生物生活在我们周围，但只能理解二维，那它就处在二维世界了吗？但在它们周围的我们却分明认为是三维，双方都是智能生物，谁对谁错！？？ 0维：没有长宽高，单纯的一个点，如奇点。 一维 只有长度 二维 平面世界 只有长宽 三维 长宽高 立体世界 我们肉眼亲身感觉到看到的世界 三维空间是点的位置由三个坐标决定的空间。客观存在的现实空间就是三维空间，具有长、宽、高三种度量。数学、物理等学科中引进的多维空间概念，是在三维空间基础上所作的科学抽象。 四维 一个时空的概念 日常生活所提及的“四维空间”，大多数都是指阿尔伯特·爱因斯坦在他的《广义相对论》和《狭义相对论》中提及的“四维时空”概念。我们的宇宙是由时间和空间构成。时空的关系，是在空间的架构上比普通三维空间的长、宽、高三条轴外又加了一条时间轴，而这条时间的轴是一条虚数值的轴。根据阿尔伯特·爱因斯坦相对论所说：我们生活中所面对的三维空间加上时间构成所谓四维空间。 一维是线，二维是面，三维是静态空间，四维是动态空间（因为有了时间）。 我们在物理学中描述某一变化着的事件时 所必须的变化的参数。这个参数就叫做维。几个参数就是几个维。比如描述“门”的位置就只需要角度所以是一维的 而不是二维 简单地说：0维是点，没有长、宽、高。一维是由无数的点组成的一条线，只有长度，没有宽、高。二维是由无数的线组成的面，有长、宽没有高。三维是由无数的面组成的体，有长宽高。维可以理解成方向。 因为人的眼睛只能看到三维，所以三维以上很难解释。正如一个智力正常,先天没有一只眼睛,一只耳朵的人(太悲哀了.这样就没有双眼效应,双耳效应),他就很难理解距离了,他很可能认为这个世界是2维的. 一个简单的说法：N维就是N条直线两两垂直所形成的空间 因为，人类只能理解到３维，所以后面的维度可以通过数学理论构建，但要仔细理解就很难.在量子力学,目前仍在建立的膜理论,认为世界是11维的.

对！
你没提起也没人注意到。

0D - a dot
1D - a line
2D - a flat surface
3D - an object (space)
4D - space-time
.
.
.
.
10 / 11D - ... ...

读了一本著名的书说，我们活着的宇宙其实是多维的。（共高达10或11维）
这些其他的为存在着只是我们无法体会到而已。

没关系。
就是如此。

最后还是要谢谢你供应的资料。是个很好的资料。但，本人也还没真正消化它（给我写时间）。读完了在回帖我的想法。加油。

mayhem_666

原帖由 'e-liang' 于 4-7-2007 05:21 PM 发表
对！
你没提起也没人注意到。

0D - a dot
1D - a line
2D - a flat surface
3D - an object (space)
4D - space-time
.
.
.
.
10 / 11D - ... ...

读了一本著名的书说，我们活着的宇宙其实 ...

是不是 brian greene 的作品？

。。看过他的纪录片。  string theory。

rEborN12

是关于维度空间的吗？？

mayhem_666

原帖由 rEborN12 于 7-7-2007 01:42 AM 发表
是关于维度空间的吗？？

有提到。而且息息相关。

没有听过你说的什么brian greene作品。

那是我是从老师那边知道的。

kimsiang

其实我们能看到东西，能触摸到东西，全都是拜赐相互作用(Interaction)。而这些就直接关系到力的强度。
我们都牛顿的万有引力(F=GMm/r^2),Coulomb的电磁力(F=kQq/r^2)等等。而他们正好都是逆2乘定理(inverse squared law)。那么，我们来想一想，如果他们都是逆3乘定理，逆6乘定理之类的话，会怎么样？
最直接的答案呢就是:力在短距离之内消失！
（举例:r=10的话，逆2乘定理 : 1/100
                 逆3乘定理 : 1/1000
                 逆6乘定理 : 1/1000000 ）
这也是为什么物理学家一直相信会有高次元的世界。他们所存在的空间太小了，需要很高的能量才能找到他们。
还有别说逆3乘定理，逆6乘定理之类的，就说强相互作用(strong interaction)的potential（Yukawa Potential）,也就是exp[-ar]/r，在核子以外的距离(10^-15 m 左右)是不会被发现的。
所以呢，生物体在逆2乘定理的世界(4维空间)之下恰到好处，能够存在。