|
查看: 1468|回复: 10
|
感叹号!Factorial :)
[复制链接]
|
|
|
之前看到每周一题出 y^2 = 1! + 2! + 3! + ... + n! 的题目。我也有一题挺不错的 
求正整数 a,b,c ,使到
a!b! = a! + b! + c!
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-12-2006 07:26 PM
|
显示全部楼层
发表于 19-12-2006 07:26 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-12-2006 11:01 AM
|
显示全部楼层
原帖由 chiaweiwoo1 于 19-12-2006 07:26 PM 发表
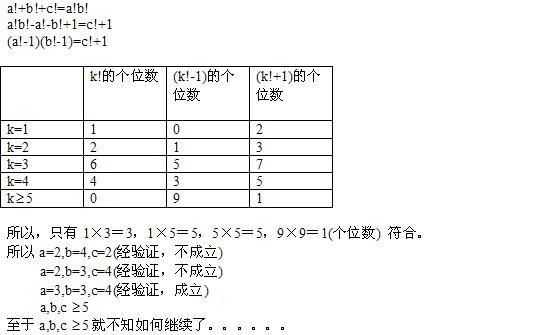
a=b=3 , c=4 的却是唯一的一幅答案。
我的做法是先证明一定要 a = b 才有解。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-12-2006 04:52 PM
|
显示全部楼层
发表于 25-12-2006 04:52 PM
|
显示全部楼层
继续。。。。。。。
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-12-2006 06:07 PM
|
显示全部楼层
当 a = b ,
(a!)^2 = 2a! + c!
=> a!(a!-2) = c!
注意到 gcd(a!,a!-2) = 2  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-12-2006 06:15 PM
|
显示全部楼层
发表于 25-12-2006 06:15 PM
|
显示全部楼层
原帖由 chiaweiwoo1 于 25-12-2006 04:52 PM 发表
继续。。。。。。。

我是用quadratic formula 来算,后来拿到 a!=1+sqrt(1+c!)
4个连续数相乘后加1,会形成一个完全平方数,所以 c可能是4或5。
然后淘汰5,c=4,a=b=3。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-12-2006 06:51 PM
|
显示全部楼层
原帖由 bomber27 于 25-12-2006 06:15 PM 发表
我是用quadratic formula 来算,后来拿到 a!=1+sqrt(1+c!)
4个连续数相乘后加1,会形成一个完全平方数,所以 c可能是4或5。
然后淘汰5,c=4,a=b=3。
4 个连续整数的积 + 1 的却是 square number . 但并不表示 n (=/= 4 )个连续整数的积 + 1 一定不是 square number  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-12-2006 06:57 PM
|
显示全部楼层
发表于 25-12-2006 06:57 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-12-2006 07:08 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-12-2006 07:41 PM
|
显示全部楼层
发表于 25-12-2006 07:41 PM
|
显示全部楼层
dunwan2tellu怎样证明a=b啊?我的证明太长了。。。。。。。
[ 本帖最后由 chiaweiwoo1 于 25-12-2006 07:49 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-12-2006 08:03 PM
|
显示全部楼层
好吧,我的方法其实和你的idea 差不多
let a = min{a,b} then from a!+b!+c!=a!b! we must have c >= a (考虑 mod a! )
(a!-1)b! - c! = a!
if b > c then c![(a!-1)k - 1] = a! where k = b!/c!
所以必须要 c = a ,也就是 (a!-1)k = 2 ,不过无解(因为必须 a=c=2 , 得到 b!=4)
所以 b =< c 从而 b![(a!-1) - m] = a! , where m = c!/b!
那么就必须有 b = a (因为 b >= a) |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|