Series:级数难题(****)

dunwan2tellu

今天翻看旧题目，发现到这题，不过已经忘了怎么做，有谁有头绪？

题目：
求级数的值

Sum[m=0 -> infinity] Sum[n=m -> infinity] (2^m * 3^n)/(m+n)! = ?



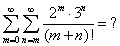
[ 本帖最后由 dunwan2tellu 于 9-8-2006 10:49 PM 编辑 ]

铁蛋

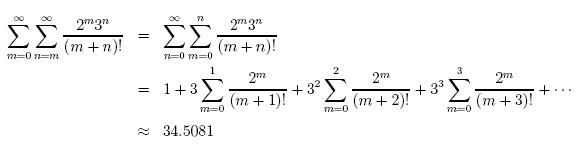
可惜没有更简单的形式了。如果直接做要用到特别函数，很多人可能不熟悉，所以把递增的秩序交换（其实只是把原本的 column sum 变成 row sum）.

dunwan2tellu

你的答案对了。要准确的话就是

3exp(3) - (1+sqrt[6]/2)exp(sqrt[6]) + (sqrt[6]/2-1)exp(-sqrt[6])

我想问你最后一步如何求得？我看不出有最后一步有什么特征。

铁蛋

噢，有这个形式？请问是怎么弄的?

最后的部分只是取足够项直到数值＂稳定＂下来，因为这个级数肯定收敛。当然要用到计算器啦。。。(mathematica)

[大师]

原帖由 dunwan2tellu 于 10-8-2006 02:55 PM 发表
你的答案对了。要准确的话就是

3exp(3) - (1+sqrt/2)exp(sqrt) + (sqrt/2-1)exp(-sqrt)

我想问你最后一步如何求得？我看不出有最后一步有什么特征。

照这算，怎么我得到58.6381555？？？

dunwan2tellu

原帖由 [大师] 于 10-8-2006 10:37 PM 发表

照这算，怎么我得到58.6381555？？？

你仔细算看。我得到的是 34.50805142...

[大师]

原帖由 dunwan2tellu 于 11-8-2006 07:09 AM 发表


你仔细算看。我得到的是 34.50805142...

用Windows 内附的caculator算也是58.638155501981032694702747628796

是不是那里出错了？

dunwan2tellu

原帖由 [大师] 于 11-8-2006 01:51 PM 发表

用Windows 内附的caculator算也是58.638155501981032694702747628796

是不是那里出错了？

你确定输入对的号码？
我用 hyperbolic function 来找，得到

3(cosh 3 + sinh 3) -2cosh(sqrt[6]) - sqrt[6]sinh(sqrt[6]) [如果没记错的话]

上面的答案我只是把他写成 exp 的 form 而已

铁蛋

原帖由 铁蛋 于 10-8-2006 09:42 AM 发表


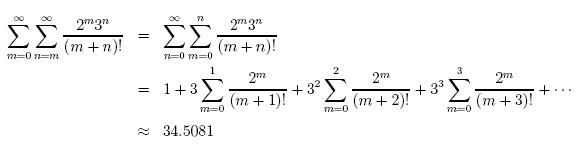
3(cosh 3 + sinh 3) -2cosh(sqrt[6]) - sqrt[6]sinh(sqrt[6])

看来是把第二行的项排一下得到的结果。。。（绝对收敛的原因）

可是太懒惰做了。。。

dunwan2tellu

我所记得的方法是先把同样的分母 group 在一起，那么我们就可以写成

Sum[i=0->oo]Sum[k=0->i]  { 2^(i-k)*3^(i+k)/(2i)! + 2^(i-k)*3^(i+k+1)/(2i+1)!}

然后用 geometric progression 来去掉 k , 然后再用hyperbolic 来表示剩下的term.

其实我想知道你用什么方法得到 34.5081 ... ?

[大师]

原帖由 dunwan2tellu 于 11-8-2006 03:00 PM 发表


你确定输入对的号码？
我用 hyperbolic function 来找，得到

3(cosh 3 + sinh 3) -2cosh(sqrt) - sqrtsinh(sqrt)

上面的答案我只是把他写成 exp 的 form 而已

哈，看到你写hyperbolic function我就知道错在那里了。。

我把你写的exp当成^了。应该是e才对。