|
查看: 2806|回复: 24
|
新加坡A level考题,STPM的可以进来试试看 [开始不断更新]
[复制链接]
|
|
|
分享手头上的资料,正考STPM可以试试看


[ 本帖最后由 無聊人 于 8-5-2006 06:43 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-4-2006 05:55 PM
|
显示全部楼层
发表于 20-4-2006 05:55 PM
|
显示全部楼层
第一题,最后一 part 还没想到....
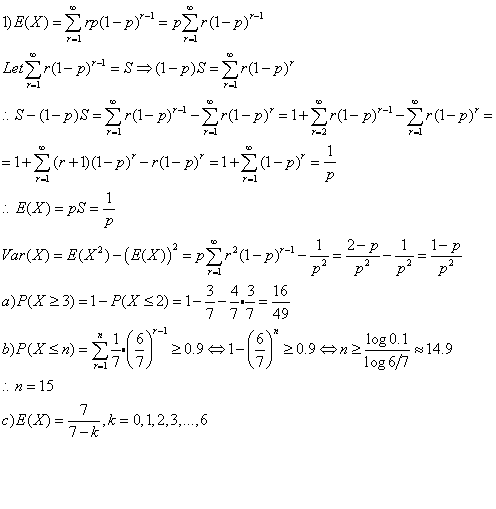 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-4-2006 06:00 PM
|
显示全部楼层
发表于 20-4-2006 06:00 PM
|
显示全部楼层
wa..有考binomial expansion!?
好像真得有点难。。。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-4-2006 06:17 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-4-2006 05:55 PM 发表
第一题,最后一 part 还没想到....
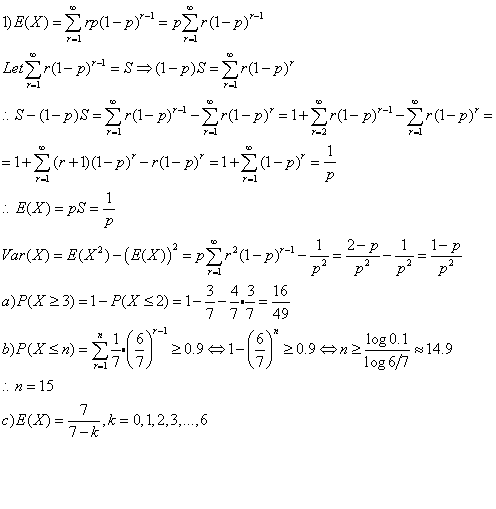
都对!加油! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-4-2006 06:18 PM
|
显示全部楼层
原帖由 又是萧晨 于 20-4-2006 06:00 PM 发表
wa..有考binomial expansion!?
好像真得有点难。。。
其实都不会难的
因为binomial expansion在中学就学过了啊! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-4-2006 06:39 PM
|
显示全部楼层
发表于 20-4-2006 06:39 PM
|
显示全部楼层
Question 2 :
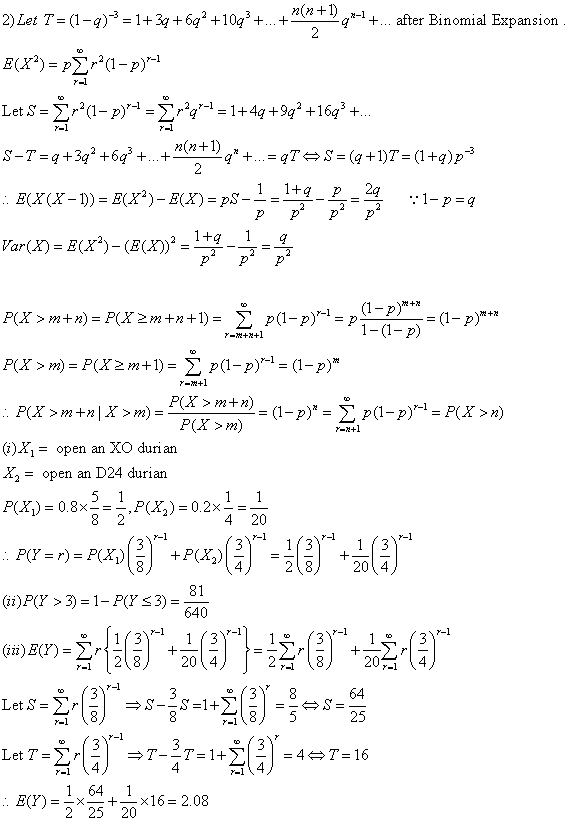 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-4-2006 06:48 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-4-2006 06:39 PM 发表
Question 2 :
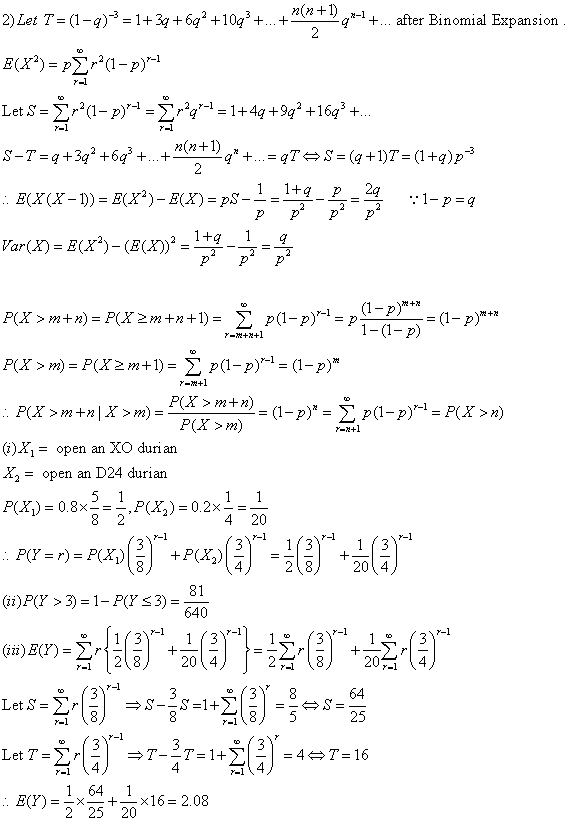
答案对了
不过第2题的proving 问题
其实有更简短的做法,我看了也比较明白
我会再贴其他的问题的,敬请期待
[ 本帖最后由 無聊人 于 20-4-2006 06:49 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-4-2006 06:52 PM
|
显示全部楼层
发表于 20-4-2006 06:52 PM
|
显示全部楼层
原帖由 無聊人 于 20-4-2006 06:48 PM 发表
答案对了
不过第2题的proving 问题
其实有更简短的做法,我看了也比较明白
我会再贴其他的问题的,敬请期待
我也觉得奇怪为何那个 proving 的只给 3 分。
目前还想不到更简短的方法。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-4-2006 07:02 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 20-4-2006 06:52 PM 发表
我也觉得奇怪为何那个 proving 的只给 3 分。
目前还想不到更简短的方法。
因为这份试卷是我老师给我做的
而我老师是从其他初级学院的试卷拿来的
3分你都好偷笑了
那间初级学院才给1分! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 21-4-2006 03:49 PM
|
显示全部楼层
发表于 21-4-2006 03:49 PM
|
显示全部楼层
第一题最后一 part
E(X) = E(0)+E(1)+E(2)+E(3)+E(4)+E(5)+E(6)
= 1+7/6 + 7/5 + 7/4 + 7/3 + 7/2 + 7/1
= 18.15 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 21-4-2006 06:35 PM
|
显示全部楼层
原帖由 dunwan2tellu 于 21-4-2006 03:49 PM 发表
第一题最后一 part
E(X) = E(0)+E(1)+E(2)+E(3)+E(4)+E(5)+E(6)
= 1+7/6 + 7/5 + 7/4 + 7/3 + 7/2 + 7/1
= 18.15
对了!
这题很容易的
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-4-2006 11:29 AM
|
显示全部楼层
发表于 22-4-2006 11:29 AM
|
显示全部楼层
典型的complex number 题目..
先用binomial expansion 求得
(c + is)^5 = c^5 - 10c^3s^2 + 5cs^4 + i(5c^4s -10c^2s^3+s^5)
之后用 De Moivre 得到 (c+is)^5 = cos 5x + isin 5x 然后 equating real and imaginary part
cos 5x = c^5 - 10c^3s^2
sin 5x = 5c^4s -10c^2s^3+s^5
所以 tan 5x = (c^5 - 10c^3s^2)/(5c^4s -10c^2s^3+s^5)
分母分子分别除于 c^5 则得证。
观察上面的 identity , 把 theta = pi/20 substitute 进去得到
1 = (5t-10t^3+t^5)/(1-10t^2+5t^4)
<==> t^5-5t^4-10t^3+10t^2+5t-1=0
<==>(t-1)(t^4-4t^3-14t^2-4t+1)=0
因为 t =/= 1 所以 t^4-4t^3-14t^2-4t+1=0 的 root 有 tan pi/20
从 tan 5x = 1 得知 5x = pi/4 + n*pi , where n = integer
==> x = (4n+1)*pi/20
因为 -pi/2 < x < pi/2 所以 n 只可以取 n = -2,-1,0,1,2 .
不过 t=1 不是root 之一, 所以淘汰 n = 1
==> t = tan [ (4n+1)*pi/20 ] , n = -2,-1,0,2 是
t^4-4t^3-14t^2-4t+1=0 的根
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 22-4-2006 02:03 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-4-2006 03:04 PM
|
显示全部楼层
发表于 22-4-2006 03:04 PM
|
显示全部楼层
从韦达定理得知
a+b+c = k
ab+bc+ac = 0
abc = 1
(1+a^4)bc + (1+b^4)ac + (1+c^4)ab = abc(a^3+b^3+c^3) + (ab+ac+bc) = 4
但a^3 + b^3 + c^3 = (a+b+c)(a^2+b^2+c^2-ab-ac-bc) + 3abc
= (a+b+c)[(a+b+c)^2 - 3(ab+bc+ac)] + 3abc
= k(k^2 - 0) + 3
所以 k^3 + 3 =4
k^3 - 1 = 0
(k-1)(k^2+k+1) = 0
得k=1 ( k^2+k+1>0 ) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-4-2006 06:50 PM
|
显示全部楼层

一间有名的初级学院试卷 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 25-4-2006 06:17 PM
|
显示全部楼层
发表于 25-4-2006 06:17 PM
|
显示全部楼层
如果没错的话 a) 可以用 Integration By Part
E(X) = $ x d^2y/dx^2 dx = [ x dy/dx ] - $ dy/dx dx = [x dy/dx] - [ y ]
因为 dy/dx = e^(-3x){2x-3x^2}
所以 [ x dy/dx ] = 1/3 * e^(-1) { 1/3 } = 1/9 * e^(-1)
[ y ] = 1/9 * e^(-1)
所以 E(X) = 0
b)也是用 Integration By Part (integrate sqrt{3a-x} 的部分之类的。
b) (ii) 可以用 substitution sqrt{3a-x} = t 和 t = sqrt{3a}sin p 所以就容易看出为何 arcsin 那咚咚会出现。
(iii)还没有“爱碟儿”如何得到 centroid ...
[ 本帖最后由 dunwan2tellu 于 25-4-2006 06:20 PM 编辑 ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 8-5-2006 06:42 PM
|
显示全部楼层
不好意思几天没有新的问题发问
因为我在等着2005年新加坡各个JC的试题
这题是我JC出的
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 10-5-2006 07:07 PM
|
显示全部楼层
发表于 10-5-2006 07:07 PM
|
显示全部楼层
a) z^9 = cos 2k*pi + isin 2k*pi ==> z = cos 2k/9*pi + isin2k/9*pi , k=-4,-3,-2...,2,3,4
e^(ia)+e^(-ia) = (cos a + isin a) + (cos a - isin a)=2cos a
z^9-1=(z-1)(z-x1)(z-x2)..(z-x8) where xk = cos 2k/9*pi + isin2k/9*pi
Also (z-x1)(z-x8) = z^2 - 2cos 2k/9*pi + 1
==> z^8+z^7+...+z+1=(z^2-2cos 2pi/9 +1)(z^2-2cos 4pi/9 +1)(z^2-2cos 2pi/3 +1)(z^2 -2cos 8pi/9 + 1)
(ii)e^(ia) = z = cos a + i sin a ==> (2z/5)^r = (2/5)^r * e^(iar)
...... |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-5-2006 12:22 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-5-2006 01:15 AM
|
显示全部楼层
发表于 19-5-2006 01:15 AM
|
显示全部楼层
原帖由 無聊人 于 19-5-2006 12:22 AM 发表
来一点比较容易的
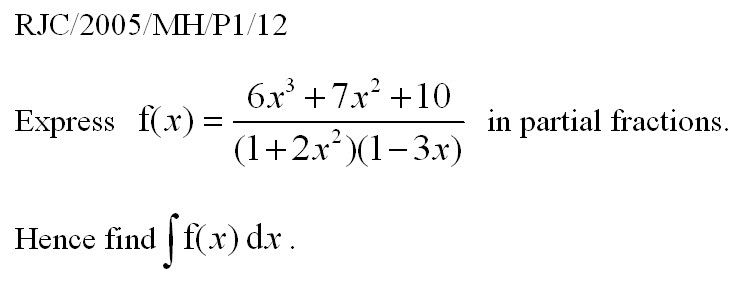

Further Maths问题
[IMG]h ...
好深哦!
不知道这是mathematics S or T ?
因为我刚上lower six,所以请多多指教。
请问你可以贴上form 6 math-S的Note吗?
我很想早一点学。。。。。。
因为老师还没开始上课。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|