|
查看: 8884|回复: 133
|
初等不等式训练(题目在第1页)
[复制链接]
|
|
|

楼主 |
发表于 17-6-2005 10:27 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-6-2005 12:27 PM
|
显示全部楼层
发表于 17-6-2005 12:27 PM
|
显示全部楼层
[1] 取 x_1 = x, x_2 = 1/x, n=2 ;
[2] 左手边 = (x^2 + 1) / √(x^2 + 1) + 1 / √(x^2 + 1)
= √(x^2 + 1) + 1 / √(x^2 + 1)
取 u = √(x^2 + 1), 引用 [1] 即解 .
[3] 排一下再引用 [1] 即解 (取 u = x^2).
原谅铁蛋吧!
 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-6-2005 05:31 PM
|
显示全部楼层
发表于 17-6-2005 05:31 PM
|
显示全部楼层
pipi 于 17-6-2005 10:27 说 :
那由 AM-GM 不等式, 我们可以先来玩玩以下的问题
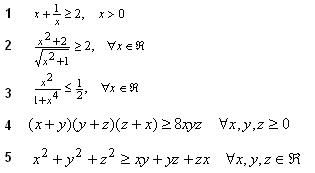
我会不时在此贴编辑,敬请大家留意,谢谢!!

pipi歡迎回來
這裡現在好冷清///
你開這個專欄不錯
我學校只學普通的不等式沒學算幾
因為老師說沒有考...
現在總算有人教了 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-6-2005 08:23 PM
|
显示全部楼层
发表于 17-6-2005 08:23 PM
|
显示全部楼层
灰羊 于 17-6-2005 17:31 说 :

pipi歡迎回來
這裡現在好冷清///
你開這個專欄不錯
我學校只學普通的不等式沒學算幾
因為老師說沒有考...
現在總算有人教了
第三題
 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 17-6-2005 08:34 PM
|
显示全部楼层
铁兄,你又来凑一脚了...
灰羊,谢谢你的支持!!
大家也来试试以下的吧!!
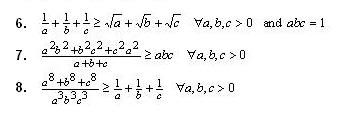 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-6-2005 11:17 PM
|
显示全部楼层
发表于 17-6-2005 11:17 PM
|
显示全部楼层
pipi 于 17-6-2005 08:34 PM 说 :
铁兄,你又来凑一脚了...
灰羊,谢谢你的支持!!
大家也来试试以下的吧!!
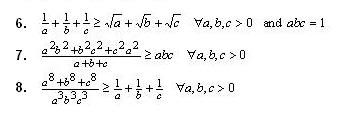
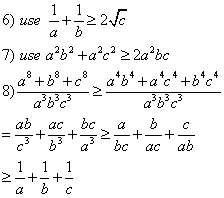 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 17-6-2005 11:22 PM
|
显示全部楼层
发表于 17-6-2005 11:22 PM
|
显示全部楼层
pipi老师,你回来了啊!
如果过后忙的话,可以选题然后我代你贴上来 ;-) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 12:06 AM
|
显示全部楼层
发表于 18-6-2005 12:06 AM
|
显示全部楼层
pipi 于 17-6-2005 20:34 说 :
铁兄,你又来凑一脚了...
灰羊,谢谢你的支持!!
大家也来试试以下的吧!!
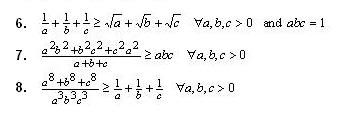
有快點的方法嗎?

[ Last edited by 灰羊 on 18-6-2005 at 03:15 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 12:12 AM
|
显示全部楼层
发表于 18-6-2005 12:12 AM
|
显示全部楼层
就是咯。。。第八题我也是解得挺长的。。。不过我偷吃太多步了 
[ Last edited by dunwan2tellu on 18-6-2005 at 04:13 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 18-6-2005 09:19 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 03:18 PM
|
显示全部楼层
发表于 18-6-2005 03:18 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 03:40 PM
|
显示全部楼层
发表于 18-6-2005 03:40 PM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 03:46 PM
|
显示全部楼层
发表于 18-6-2005 03:46 PM
|
显示全部楼层
pipi 于 18-6-2005 09:19 AM 说 :
不错!不错!题目会越来越好玩。暂时试试:
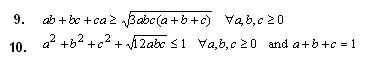
我 来 试 第9 题
设 x=ab , y=ac , z=bc
(x+y+z)^2 = x^2 +y^2 + z^2 + 2(xy +yz+xz)
>=(xy+yx+xz) + 2 (xy+yz+xz) ( 用x^2+y^2>=2xy )
=3(xy + yz + xz )
得 x+y+z >= sqrt {3(xy+xz+yz)}
将a,b,c 带 入 即 可 得 不 等 式
[ Last edited by dunwan2tellu on 18-6-2005 at 03:48 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 04:09 PM
|
显示全部楼层
发表于 18-6-2005 04:09 PM
|
显示全部楼层
dunwan2tellu 于 18-6-2005 15:46 说 :
我 来 试 第9 题
设 x=ab , y=ac , z=bc
(x+y+z)^2 = x^2 +y^2 + z^2 + 2(xy +yz+xz)
>=(xy+yx+xz) + 2 (xy+yz+xz) ( 用x^2+y^2>=2xy )
=3(xy + yz + x ...
原來dunwan2tellu已經想到更好的方法.... |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 04:13 PM
|
显示全部楼层
发表于 18-6-2005 04:13 PM
|
显示全部楼层
以下是算幾不等式的加權形式

原來tiny的圖只能放一天
[ Last edited by 灰羊 on 19-6-2005 at 02:13 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 18-6-2005 04:18 PM
|
显示全部楼层
发表于 18-6-2005 04:18 PM
|
显示全部楼层
灰羊 于 18-6-2005 04:09 PM 说 :
原來dunwan2tellu已經想到更好的方法....
其 实 大 质 上 一 样。
灰羊 于 18-6-2005 04:13 PM 说 :
以下是算幾不等式的加權形式

[ Last edited by 灰羊 on 18-6-2005 at 04:15 PM ]
 好 不 错 的 一 个 不 等 式 好 不 错 的 一 个 不 等 式
[ Last edited by dunwan2tellu on 18-6-2005 at 04:28 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-6-2005 12:31 PM
|
显示全部楼层
发表于 19-6-2005 12:31 PM
|
显示全部楼层
这里有几题不等试
1)a,b,c为三角形的三边,试证明
√(a + b - c) + √(b + c - a) + √(c + a - b) ≤ √a + √b + √c
2) 若a,b,c >0 且 满 足 1/a + 1/b + 1/c = 1 , 试 证 明
√(a + bc) + √(b + ca) + √(c + ab) ≥ √(abc) + √a + √b + √c
欢迎大家来试
[ Last edited by dunwan2tellu on 19-6-2005 at 12:41 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 20-6-2005 09:04 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 20-6-2005 05:08 PM
|
显示全部楼层
发表于 20-6-2005 05:08 PM
|
显示全部楼层
先试试13,14
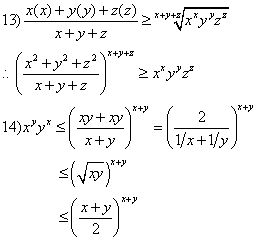 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|