公式选美

yaahoo

如果要你选出一个优美的数学公式或定理,你会选那一个?

haryewkun

1 + 1 = 2

这应该也算是数学公式。。。

多普勒效应

我选 "哥德尔不完全定理" (Godel's Incompleteness Theorem)

如果形式算术系统w无矛盾的，则存在着这样一个命题，该命题及其否定在该系统中都不能证明，亦即它是不完备的。

yaahoo

1+1=2, 美固然美,但是却是外在美,无法充分表现出算术系统的精神.

Godel不完全性定理曾被认为是上世纪其中一项最重要的发现之一.美诚美哉,可惜它却让数学从此不再完美.可恨!

这个很美吧~ e^-(i*pi) + 1 = 0 ,我打得没错罢...

yaahoo

右手 于 30-11-2004 09:57 PM  说 :
这个很美吧~ e^-(i*pi) + 1 = 0 ,我打得没错罢...

应是e^(i*Pi)+1=0

这个式子虽然只是个特例,却有很多有趣的性质.它结合了代数,几何和分析,联系着数学中的五个重要的常数.三个重要的运算,加,乘及次方.第一次学到时很兴奋,当时一直想找出这式子背后的意义,去解释它.你能说出所以然吗?

灰羊

a^2+b^2=c^2
畢達哥拉斯定理
建議開一個投票!

多普勒效应

各位先提名！
够十个再开投票站！

1. 1+1=2
2.哥德尔不完全定理
3.毕氏定理
4.e^(i*Pi)+1=0
5. sin a/cos a = tan a
6
7
8
9
10

[ Last edited by 多普勒效应 on 4-12-2004 at 07:36 PM ]

灰羊

sin/cos=tan
把三角函數的基本都用上了..

yaahoo

不妨参考一下,







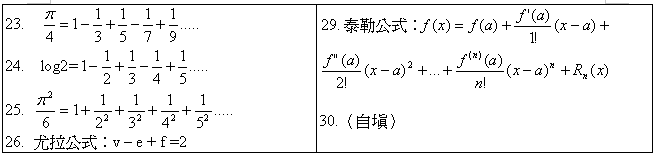
[ Last edited by yaahoo on 13-12-2004 at 11:09 PM ]

fritlizt

1+1 = 2 吧。
没有他什么都不用玩了。

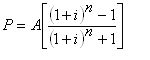
这个是Compound annual interest的公式，里头包含了+-*/，而且分子分母相当对称。

Revenge38

E=Mc^2

shoulb be the best

这是物理公式吧......

[ Last edited by 多普勒效应 on 20-12-2004 at 11:39 AM ]

灰羊

Revenge38 于 20-12-2004 10:26  说 :
E=Mc^2

shoulb be the best

这是物理公式吧......

[ Last edited by 多普勒效应 on 20-12-2004 at 11:39 AM ]

物理數學本是一家~~~^_^

灰羊

yaahoo 于 13-12-2004 23:08  说 :
不妨参考一下,







[ Last edited by yaahoo on 13-12-2004 at 11 ...

想請問你泰勒展開式的a是任意數嗎?

yaahoo

a 必须使右式都存在.也就是说 f(x) 必须够平滑,可以求导很多次.

灰羊

yaahoo 于 20-12-2004 18:21  说 :
a 必须使右式都存在.也就是说 f(x) 必须够平滑,可以求导很多次.

微分到f(x)為常數為止?
a是所有使f(x),f'(x),f''(x)....成立的數嗎?

yaahoo

f(x) 在a 附近如果有越多阶导数存在,则可以用一多项式很好的逼近它.不一定须微分到常数,如f(x)=sin x.用无穷多项可写等于,用有限多项则有R(x), 即误差.x 离 a 越远须越多项才可使误差小些. 不妨用f(x)=sinx, a =0,试试. 可得:sin x = x - x^3/3! + x^5/5! - x^7/7! +......

[ Last edited by yaahoo on 20-12-2004 at 08:52 PM ]

灰羊

yaahoo 于 20-12-2004 20:51  说 :
f(x) 在a 附近如果有越多阶导数存在,则可以用一多项式很好的逼近它.不一定须微分到常数,如f(x)=sin x.用无穷多项可写等于,用有限多项则有R(x), 即误差.x 离 a 越远须越多项才可使误差小些. 不妨用f(x)=sinx, a =0 ...

a=0
sinx=sinx + (sinx)'x/1! + (sinx)''x^2/2! .....怎麼變成
sin x = x - x^3/3! + x^5/5! - x^7/7! +......???

铁蛋

这个简单啊。。。

f(x) = sin(x) ,  在零附近展开:

f(x) = f(0) + f'(0)x + f''(0) x^2 / 2! + ...

f'(x) = cos(x), => f'(0) = 1
f''(x) = -sin(x), => f''(0) = 0
f'''(x) = -cos(x), => f'''(0) = -1
...
不难发现
f^(2n-1) (0) = (-1)^(n-1) , n=1,2,...
f^(2n) (0) = 0 , n=1,2,...

so: f(x) = x - x^3 / 3! + x^5 / 5! - ...