|
查看: 2165|回复: 17
|
大专数学训练题库
 [复制链接]
[复制链接]
|
|
|

楼主 |
发表于 12-10-2004 09:41 AM
|
显示全部楼层
22/08/2004,星期日
大专(C1) 设 p(x) = a + bx + 3cx^2 + dx^3 + 5ex^4 为一实?嘞钍健?
已知 a + c + e = 0,求证 p(x) = 0 在区间 [-1,1] 中有一实根。 (已解)
(答案:--)
(解对者:**)
解法(一)
f(1)=a + b/2 + c + d/4 + e=b/2+d/4
f(-1)=-a + b/2 - c + d/4 - e=b/2+d/4
==> f(1)=f(-1)
==> f'(x)=(f(1)-f(-1))/2=0 在区间 [-1,1] 中有一實根。 (叫"均值定理"的樣子)
==> p(x)=0 在区间 [-1,1] 中有一實根。
解法(二)
若 p(x) = 0 for all x in [-1,1],那么原题得证!
假设 p(x)≠0 for all x in [-1,1]。
那么(i) p(x) > 0 for all x in [-1,1] 或者
(ii) p(x) < 0 for all x in [-1,1]。
我们将分别从 (i)与(ii) 得到 ∫p(x) dx > 0 及 ∫p(x) dx < 0
(这与我们的计算 ∫p(x) dx = 0 产生矛盾!!)
所以存在着 r, s in [-1,1] 令到 p(r)p(s) <0 ,
由于 p(x) 是连续方程,
就存在着 k in [-1,1] 令到 p(k)=0 。(Intermediate Value Theorem)
证毕! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:43 AM
|
显示全部楼层
29/08/2004,星期日
大专(C2) 设 f(x) 为可微(differentiable)偶函数 (即 f(-x) = f(x) for all x)。求证
(i) f '(x) 为奇函数 (即 f '(-x) = - f '(x) for all x)。
(ii) f '(0) = 0 (已解)
(答案:--)
(解对者:sinchee)
(i)
解法(一)
f '(-x) = lim (h->0) [f(-x+h)-f(-x)]/h
= lim (h->0) [f(x-h)-f(x)]/h
= lim (h->0) –[f(x)-f(x-h)]/h
= - lim (h->0) [f(x)-f(x-h)]/h
= - f ’(x)
hence prove.
解法(二)
f(-x)=f(x)
f'(-x)*(-x)'=f'(x)
-f'(-x)=f'(x)
f'(-x)= -f'(x)
(ii)
f ’(0) = f ’(-0) = - f ’(0)
因此 f '(0) = 0 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:54 AM
|
显示全部楼层
29/08/2004,星期日
大专(C2)' a,b,c 为整数。
若 a^2 + b^2 + c^2 是 16 的倍数,
求证 a^3 + b^3 + c^3 是 64 的倍数。 (已解)
(答案:--)
(解对者:辉文,微中子)
考虑
任何整数被16除的余数,
0, 1, 2, ..., 15
所以,任何整数n,
n^2 = x (mod 16)
当中,x只有0,1,4,9的可能性.
为了让a^2 + b^2 + c^2 = 16m的形式
x 只能是0,
考虑其中一个a^2 = 16k
所以a = 4 sqrt(k) ,不过a 是整数,所以sqrt(k)也是整数.
所以a是4的倍数.
同理,a, b, c都是4的倍数
a = 4q, b = 4s, c = 4r, q,s,r都是整数
a^3 + b^3 + c^3 = 64(q^3 + r^3 + s^3) = 64p, p 整数
所以是64的倍数. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:56 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 09:59 AM
|
显示全部楼层
12/09/2004,星期日
大专(C4) 在边长为 2 的正六边形上任意点 25 个点。
证明:存在着两点,其距离小于 1。 (已解)
(答案:--)
(解对者:sinchee)
設沒有兩點的距离小于 1。
首先﹐將正六边形分割成大小相等﹐邊長為1的三角形。
不難發現﹐一個三角形內﹐不能存在著兩點。
因此﹐最多能放24個點。
若點上25個點﹐必存在着两点,其距离小于 1。 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:08 AM
|
显示全部楼层
19/09/2004,星期日
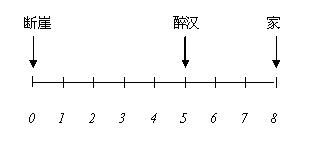
大专(C5) 某个醉汉目前在位置 "5",他的家在位置 "8",而位置 "0" 则是断崖。
由于他分不清方向,设他每次移动一单位,且只走向左或向右,而每次向左或向右的机率皆为 1/2。
若到位置 "8",则家人迎接他(安全抵达)。
若到位置 "0", 则跌入断崖。。。(无法继续行程)
求此醉汉安全回到家的机率。
 (已解) (已解)
(答案:5/8)
(解对者:sinchee,斷羽鳥)
解法(一)
設 0 為斷崖的位置﹐ P(k,n) 為從 k 安全 n 到的概率。
則 P(1,2) = 1/2
P(2,3) = 1/2 + 1/2[P(1,2)][P(2,3)]
=> P(2,3) = 2/3
P(3,4) = 1/2 + 1/2[P(2,3)][P(3,4)]
=> P(3,4) = 3/4
P(4,5) = 1/2 + 1/2[P(3,4)][P(4,5)]
=> P(4,5) = 4/5
P(5,6) = 1/2 + 1/2[P(4,5)][P(5,6)]
=> P(5,6) = 5/6
P(6,7) = 1/2 + 1/2[P(5,6)][P(6,7)]
=> P(6,7) = 6/7
P(7,8) = 1/2 + 1/2[P(6,7)][P(7,8)]
=> P(7,8) = 7/8
因此﹐P(5,8) = [P(5,6)] [P(6,7)] [P(7,8)]
= 5/8
解法(二)
t + 1
0 1 2 3 4 5 6 7 8
---------------------------------
0 | 1
1 | .5 .5
2 | .5 .5
3 | .5 .5
4 | .5 .5
t 5 | .5 .5
6 | .5 .5
7 | .5 .5
8 | 1
這基本上是一個Random Markov Chains. 我們可把醉漢的步伐用上面的 transition probability matrix 來代表. 那有兩的absorbing state … 就是 8 和 0 嘛!
如果說 ui = Pr( X(t =T) = 8 | X(t = 0) = i), 那麽我要找的就是 u5 咯! 可用Markov Chain Theory 裏的 First Step Analysis 來解!.
u0 = 0 (永遠到不了傢咯) ; u8 = 1 咯! 對吧! 接下來我們有.
u1 = 0.5*u0 + 0.5*u2 = 0.5*u2
u2 = 0.5*u1 + 0.5*u3
u3 = 0.5*u2 + 0.5*u4
u4 = 0.5*u3 + 0.5*u5
u5 = 0.5*u4 + 0.5*u6
u6 = 0.5*u5 + 0.5*u7
u7 = 0.5*u6 + 0.5*u8 = 0.5*u6 + 0.5
Solve the equations system => u5 = 5/8
REMARK:
比較Genaral的case :
用數學歸納法﹐
證明﹕P(n-1,n) = (n-1)/n
P(1,2) = 1/2
設 P(k-1,k) = (k-1)/k,
則 P(k,k+1) = 1/2 + 1/2 [P(k-1,k)] [P(k,k+1)]
=> P(k,k+1) = k/(k+1)
因此﹐ P(n-1,n) = (n-1)/n (得証)
故 P(k,n) = [P(k,k+1)][P(k+1,k+2)]…[P(n-1,n)]
= [k/(k+1)][(k+1)/(k+2)]…[(n-1)/n]
= k/n
[ Last edited by pipi on 12-10-2004 at 12:04 PM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 10:10 AM
|
显示全部楼层
26/09/2004,星期日
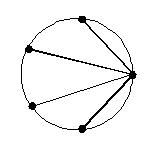
大专(C6) 如下图,在单位圆(即半径为 1)的圆周上取 5 个点。
(将这5点连起来,可形成正五边形)
现在,5 点中任选 1 点,将此点接连其余 4 点,得四个线段.
设这四个线段的长度分别为 a,b,c,d。
求证: abcd = 5
 (已解) (已解)
(答案:--)
(解对者:止战之殇,fritlizt)
解法(一)
角度ABC = 角度 BCD = 角度 CDE = 角度 DEA = 角度 EAB = (5-3)(180)/5 = 108度
b = c (因为角度 BCD = 角度 AED, CD = ED, BC = AE)
把ABCDE五点都连接到圆圈中心点 O,
角度 AOB = 角度 BOC = 角度 COD = 角度 DOE = 角度 EOA = 360/5 = 72度
d^2 = 1^2 + 1^2 – 2(1)(1)cos72
= 2 – 2cos72
c^2 = d^2 + d^2 – 2(d)(d)cos108
= 2d^2[1 – cos108]
= 2[2 – 2cos72][1 – cos108]
abcd = (bc)(ad)
= (c^2)(d^2) (因为 b = c, a = d)
= 2[2 – 2cos72][1 – cos108] [2 – 2cos72]
= 2[(2 – 2cos72)^2] [1 – cos108]
= 5
解法(二)
因为 cos72 = {sqrt(5)-1}/4
cos 144 = -{sqrt(5)+1}/4
a^2 =1^2+1^2-2(1)(1)cos72
=2-{sqrt(5)-1}/2
={5-sqrt(5)}/2
b^2 = 1^2+1^2-2(1)(1)cos144
= 2+{sqrt(5)+1}/2
={5+sqrt(5)}/2
c = b
d = a
abcd = a^2*b^2
= {5-sqrt(5)}/2 * {5+sqrt(5)}/2
= {5+sqrt(5)}{5-sqrt(5)} /4
= 20/4
= 5
[ Last edited by pipi on 12-10-2004 at 11:47 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:20 PM
|
显示全部楼层
03/10/2004,星期日
大专(C7)
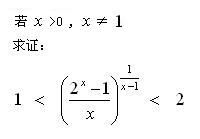
( 提示:利用 Mean Value Theorem ) (待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 12-10-2004 12:22 PM
|
显示全部楼层
10/10/2004,星期日
大专(C8)
 (已解) (已解)
(答案:--)
(解对者:情~風)
(a)
n + Sn
= n + 1 + 1/2 + ... + 1/n
= (1+1) + (1+ 1/2) + ... + (1+ 1/n)
= 2 + 3/2 + 4/3 + 5/4 + ... + (n+1)/n
≥ n{(2)(3/2)(4/3)...[(n+1)/n]}^(1/n) by AM-GM inequality
= n(n+1)^(1/n)
Since 2 ≠ 3/2 ≠ ... ≠ (n+1)/n, so the equality won’t hold.
Thus n + Sn > n(n+1)^(1/n).
Method for (b) is similar to that of (a).
n - Sn
= n - 1 - 1/2 - ... - 1/n
=(1-1) + (1- 1/2) + (1-1/3) + ... + (1- 1/n)
= 1/2 + 2/3 + 3/4 + ... + (n-1)/n
≥ (n-1){(1/2)(2/3)(3/4)...[(n-1)/n]}^[1/(n-1)] by AM-GM inequality
= (n-1)(1/n)^[1/(n-1)]
= (n-1)n^[-1/(n-1)].
Since 1/2 ≠ 2/3 ≠ ... ≠ (n-1)/n, so the equality wont hold.
So n - Sn > (n-1)n^[-1/(n-1)].
[ Last edited by pipi on 15-10-2004 at 11:09 AM ] |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 19-10-2004 10:30 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 25-10-2004 03:57 PM
|
显示全部楼层
24/10/2004,星期日
大专(C10) 若 0 < x ,y < 1 。
求证 1 < x^y + y^x < 2 。 (待解)
(答案:)
(解对者:) |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 30-10-2004 07:39 PM
|
显示全部楼层
24/10/2004,星期日
大专(C11)
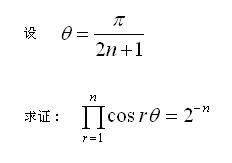 (待解) (待解)
(答案:--)
(解对者:sinchee)
解法:

[ Last edited by 多普勒效应 on 5-11-2004 at 08:31 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-11-2004 08:28 PM
|
显示全部楼层
发表于 5-11-2004 08:28 PM
|
显示全部楼层
07/11/2004,星期日
大专 (C12)
一间工厂生产两种口味的糖果:草莓和香草。我们无法从糖果的表面判断糖果的口味。有关的糖果将会包装成包裹。每种包裹里的组合都可能不一样(可能整包都是草莓口味的糖果或是整包都是香草口味的糖果,或是一颗草莓其余香草等等)。假设每包糖果的数量都一样以及每种组合的机率都一样。
小明买了一包有关的糖果,尝了一颗发觉是草莓口味。如果现在小明取第二颗糖果(第一颗没放回去),请问第二颗糖果是草莓口味的机率是多少?
(已解)
(答案:2/3)
(解对者:sinchee,萧晨)
[ Last edited by 多普勒效应 on 7-11-2004 at 03:05 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:11 AM
|
显示全部楼层
发表于 19-11-2004 12:11 AM
|
显示全部楼层
14/11/2004,星期日
大专 (C13)
证明 2≤ (1 + 1/n)^n <3
如果 n 是任何 自然数。
(已解)
(答案:-)
(解对者:)
(感谢 flash 提供)
解法(一)
画图法:
首先,(1 + 1/n)^n and n is natural number
可以化为(1 + k)^(1/k) and 0<k<1
then draw 3 lines--->y=1+k
y=2^k
y=3^k
可以发现在0<k<1里面
y=2^k一直都在y=1+k之下---->很简单,不用画图出来也知道啦。。。(因为只有在k=0,k=1相交)
y=3^k一直都在y=1+k之上 (因为两个交点,一个是k=0,一个是k<0)
2^k<1+k<3^k
===>2<(1+k)^(1/k)<3 当0<k<1
===>2<(1 + 1/n)^n<3 当n is natural number
(可以这样变换因为n is natural number 的range在0<k<1的domain里面)
解法(二)
证明(1+1/n)^n-2>0,(1+1/n)^n-3<0
(1+1/n)^n-2
=[(1+n)/n]^n-2
=[(1+n)^n-2n^n]/(n^n)--------->分母先搁着一边,打字太麻烦了
=(1+n)^n-2n^n--->展开
=1+(nC1)(n)+(nC2)(n^2)+...+(nC(n-2))(n^(n-2))+(nC(n-1))(n^(n-1))+(nCn)(n^n))-2n^n
由于最后三项相加就是0-->(nC(n-1))(n^(n-1))+(nCn)(n^n))-2n^n=0
剩下的全部是正数
所以,(1+1/n)^n-2>0
(1+1/n)^n>2
然后就是证明(1+1/n)^n-3<0--->maximum=e<3
所以就解到了
解法(三)
y=(1+1/n)^n是一个monotonic increasing function(容易证明)
所以取最小n=1,y=2
取最大,用limitn-->无限,y=e
所以就解到
[ Last edited by 多普勒效应 on 4-12-2004 at 09:05 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:13 AM
|
显示全部楼层
发表于 19-11-2004 12:13 AM
|
显示全部楼层
[coloe=blue]21/11/2004,星期日
大专 (C14)
这题须要有一些赌博的知识,希望不会教坏小孩。
五个赌徒分别坐在五个赌桌玩 poker (也叫 "派"(pair))。如果五个人手上的牌分别是:
(A) A(黑桃)A(红心)A(方块)K(黑桃)K(红心)
(B) A(黑桃)A(红心)A(方块)Q(黑桃)Q(梅花)
(C) A(黑桃)A(红心)A(方块)Q(黑桃)Q(红心)
(D) A(黑桃)A(红心)A(方块)6(黑桃)6(梅花)
(E)A(黑桃)A(红心)A(方块)3(黑桃)3(梅花)
那谁赢的机会最大?(假设是用 52 张牌,没有 joker)
(已解)
(答案:D)
(解对者:sinchee)
(感谢 flash 提供)
解法
答案应该是(D)才对啦!!!
想想一下,5 个人都拿 3 个 A ,
只要有人拿 4 张相同的牌就输了,5 人输的机会都相等。
但如果有人拿同花顺,他们也会输,
而 (D) 的情况,别人拿同花顺的机会最小,
即,(D) 赢的机会最大。
[ Last edited by 多普勒效应 on 4-12-2004 at 09:08 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 19-11-2004 12:15 AM
|
显示全部楼层
发表于 19-11-2004 12:15 AM
|
显示全部楼层
28/11/2004,星期日
大专 (C15)
请算出
(cos x)^2 + (cos 2x)^2 + ... (cos nx)^2
(待解)
(答案:)
(解对者:)
(感谢 flash 提供)
[ Last edited by 多普勒效应 on 4-12-2004 at 09:08 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-12-2004 09:09 AM
|
显示全部楼层
发表于 4-12-2004 09:09 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|