|
查看: 8643|回复: 121
|
中学数学讨论区-限于课业的问题
[复制链接]
|
|
|
 发表于 4-7-2004 12:07 AM
|
显示全部楼层
发表于 4-7-2004 12:07 AM
|
显示全部楼层
你的equation写的很乱哦..
是不是
2^(2x) +64*2^(-x) = 32呢?
如果是这个的话,
(2^x) {2^(2x) +64*2^(-x)} = (2^x) 32
2^(3x) + 64 = 32 (2^x)
让 u = 2^x
2^3x = (2^x)^3 = u^3
u^3 - 32u + 64 = 0
已经知道其中一个x=2 就是u=4,
(u^3 - 32u + 64)= (u-4)(u^2 + 4u - 16) = 0
除了u=4,还有 u = (-4 + sqrt(80))/2 和 (-4 - sqrt(80))/2
然而, u <0并无real number solution for x.
所以只有 u = (-4 + sqrt(80))/2会有实数解.
2^x = (-4 + sqrt(80))/2
x = 1.306 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 4-7-2004 04:05 PM
|
显示全部楼层
微中子 于 4-7-2004 12:07 AM 说 :
你的equation写的很乱哦..
是不是
2^(2x) +64*2^(-x) = 32呢?
如果是这个的话,
(2^x) {2^(2x) +64*2^(-x)} = (2^x) 32
2^(3x) + 64 = 32 (2^x)
让 u = 2^x
2^3x = (2^x)^3 = u^3
u^3 - 32u + 64 = 0
...
对啦,对啦。你好利害哦!!
可是还有一点不明白。
为什么一开始 2^(2x) 和 32 那边要加(2^x)??
还有,-4+squa(80)/2 怎样拿到的??
sorry.......
我真的很笨。。。  |
|
|
|
|
|
|
|
|
|
|
|
 发表于 4-7-2004 05:26 PM
|
显示全部楼层
发表于 4-7-2004 05:26 PM
|
显示全部楼层
BluStAr 于 4-7-2004 04:05 PM 说 :
对啦,对啦。你好利害哦!!
可是还有一点不明白。
为什么一开始 2^(2x) 和 32 那边要加(2^x)??
还有,-4+squa(80)/2 怎样拿到的??
sorry.......
我真的很笨。。。 
其实我是乘2^x,不是加.
主要原因是我不要有2^(-x)
在那个equation里,
所以我这样做.
而且2^x不可能是零,
所以这样做是安全的.
至于(-4 + sqrt(80))/2,
sqrt代表squareroot.
这个是解u^3 - 32u + 64 = 0
这个quadratic equation拿到的.
应该有两个答案,
但是只有>0的答案才有real number x.
所以我选(-4 + sqrt(80))/2. |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 5-7-2004 02:28 PM
|
显示全部楼层
微中子 于 4-7-2004 12:07 AM 说 :
你的equation写的很乱哦..
是不是
2^(2x) +64*2^(-x) = 32呢?
如果是这个的话,
(2^x) {2^(2x) +64*2^(-x)} = (2^x) 32
2^(3x) + 64 = 32 (2^x)
让 u = 2^x
2^3x = (2^x)^3 = u^3
u^3 - 32u + 64 = 0
...
还有哦,u^3-32u+64 要变去 (u-4)(u^2+4u-16u)....有没有formula 或者shortcut??? 我不是很会“看”要怎样变。 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-7-2004 02:36 PM
|
显示全部楼层
发表于 5-7-2004 02:36 PM
|
显示全部楼层
是(u-4)(u^2+4u-16)啦
从u^3-32u+64
我们知道u=4是其中一个.
首先可以写成
(u-4)(...)
然后我们知道 u^3的coefficient = 1,
free of u的term 是64
所以我们可以写
(u-4)(u^2... -16)
然后u^2的coefficient=0
只有-4u^2 + 4u^2
所以(u-4)(u^2 + 4u - 16)
如果看不出,可以让
(u^3 - 32u + 64)= (u-4)(Au^2 + Bu + C)
然后展开(u-4)(Au^2 + Bu + C) = Au^3 + (B-4A)u^2 + (C - 4B)u -4C
然后 A = 1, C = -16, B = 4
不过这样比较慢,也比较麻烦. |
|
|
|
|
|
|
|
|
|
|
|
 发表于 5-7-2004 03:04 PM
|
显示全部楼层
发表于 5-7-2004 03:04 PM
|
显示全部楼层
知道u-4 是其中一个factor
那么 也可以用除法来找 |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 11-7-2004 01:49 PM
|
显示全部楼层
我想請問這種題目該怎麼做???
show that root of the equation z^4-16=0 are represented in an Argand diagram by the vertices of a square.
該要怎樣才可以變成 a+bi ??
given that the complex number z and its conjugate z* satisfy the equation zz*+2zi=12+6i, find the possible value of z.
謝謝!! |
|
|
|
|
|
|
|
|
|
|
|
 发表于 11-7-2004 05:20 PM
|
显示全部楼层
发表于 11-7-2004 05:20 PM
|
显示全部楼层
第一题:
是用这个吗?
x^n - c = 0 ( if c > 0)
x = [abs(c)]^(1/n) { cos [(2k*PI)/n] + i sin [(2k*PI)/n] }
so z^4 - 16 = 0
z = 2 { cos [(2k*PI)/4] + i sin [(2k*PI)/4] } k = 0,1,2,3
太久没动COMPLEX NUMBER (复数),忘了好多。。
第二题:
我找到两个:
let z = (a+ib) --> substitute into the equation, expand then find the real part and imaginary part ( sorry, can't type chinese when i 'edit' )
z = (3+3i) conjugate (共扼)-> z* = (3-3i) 或
z = (3-i), z* = (3+i)
是不是这样ah?
各位精英, 请指教。
[ Last edited by jwyong on 11-7-2004 at 06:31 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 22-7-2004 07:46 AM
|
显示全部楼层
发表于 22-7-2004 07:46 AM
|
显示全部楼层
jwyong 于 11-7-2004 05:20 PM 说 :
第一题:
是用这个吗?
x^n - c = 0 ( if c > 0)
...
是不是这样ah?
我也许久没什么动"复数"了。。。不过我想:就是这样! |
|
|
|
|
|
|
|
|
|
|
|

楼主 |
发表于 24-7-2004 01:00 AM
|
显示全部楼层
jwyong 于 11-7-2004 05:20 PM 说 :
第一题:
是用这个吗?
x^n - c = 0 ( if c > 0)
x = [abs(c)]^(1/n) { cos [(2k*PI)/n] + i sin [(2k*PI)/n] }
so z^4 - 16 = 0
z = 2 { cos [(2k*PI)/4] + i sin [(2k*PI)/4] } k = 0,1,2,3
...
第二题对了,第一题。。。。。。。。。好象不对!!
怎么好象还没作完??
还是你要我自己算?? |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2004 01:18 AM
|
显示全部楼层
发表于 24-7-2004 01:18 AM
|
显示全部楼层
第二题:
lets: z=a+bi
zz*+2zi=a^2+b^2+2(a+bi)i
= a^2 + b^2 + 2ai -2b
= (a^2 + b^2 - 2b) +2ai
= 12 + 6i
---2a = 6
a = 3
---3^2 + b^2 -2b = 12
b^2 - 2b -3 = 0
(b-3)(b+1) = 0
b = 3,-1
所以:z=3+3i, 3-i
不知我的答案有没有错,不过方法应该是对的。
[ Last edited by fritlizt on 24-7-2004 at 01:21 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 24-7-2004 01:42 AM
|
显示全部楼层
发表于 24-7-2004 01:42 AM
|
显示全部楼层
第一题,如果你把k=0,1,2,3代入z=blah..blah..那一式子,你将得4个解:
k=0时,z=2
k=1时,z=2i
k=2时,z=-2
k=3时,z=-2i
不知答案对吗?
不知道有没有更简易的方法?
For Argand Diagram, I think you need to figure out yourself. I cannot show it here. The 4 roots I get are basically in the form of a+bi.
*edit - cant type chinese*
[ Last edited by jwyong on 24-7-2004 at 01:48 AM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 28-7-2004 08:08 PM
|
显示全部楼层
发表于 28-7-2004 08:08 PM
|
显示全部楼层
请prove这一题
if a = log(10/9)
b = log(25/24)
c = log(81/80)
plz prove that log 2 = 7a-2b+3c
这题我和朋友的证明方法都不一样,我还想看看其他的高见。。。
谢谢 |
|
|
|
|
|
|
|
|
|
|
|
 发表于 29-7-2004 12:04 AM
|
显示全部楼层
发表于 29-7-2004 12:04 AM
|
显示全部楼层
来看看我的方法。
log 2 = 7a - 2b + 3c , where a = log (10/9), b = log (25/24), c = log (81/80)
7a - 2b + 3c
= 7[log (10/9)] - 2[log (25/24)] + 3[log (81/80)]
= 7(log 10 - log 9 - 2(log 25 - log 24) + 3(log 81 - log 80)
= 7(log 2 + log 5 - 2log 3) - 2[2log 5 -(log 3 + 3log 2)] + 3[4log 3 - (log 5 + 4log 2)] Note: log 9 = 2log 3
= 7log 2 + 7log 5 - 14log 3 - 4log 5 + 2log 3 +6log 2 + 12log 3 - 3log 5 - 12log 2
= log 2
= proven |
|
|
|
|
|
|
|
|
|
|
|
 发表于 30-7-2004 10:24 AM
|
显示全部楼层
发表于 30-7-2004 10:24 AM
|
显示全部楼层
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-8-2004 04:49 PM
|
显示全部楼层
发表于 6-8-2004 04:49 PM
|
显示全部楼层
一 个 关 于Pembezaan 的 题 目!!
y=punca kuasa dua x
请 用Prinsip Pertama 找 出dy/dx |
|
|
|
|
|
|
|
|
|
|
|
 发表于 6-8-2004 10:58 PM
|
显示全部楼层
发表于 6-8-2004 10:58 PM
|
显示全部楼层
什么是Prinsip Pertama?
y=x^(1/2)
dy/dx=(1/2)x^(-1/2) |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-8-2004 07:06 AM
|
显示全部楼层
发表于 7-8-2004 07:06 AM
|
显示全部楼层
我的解答:
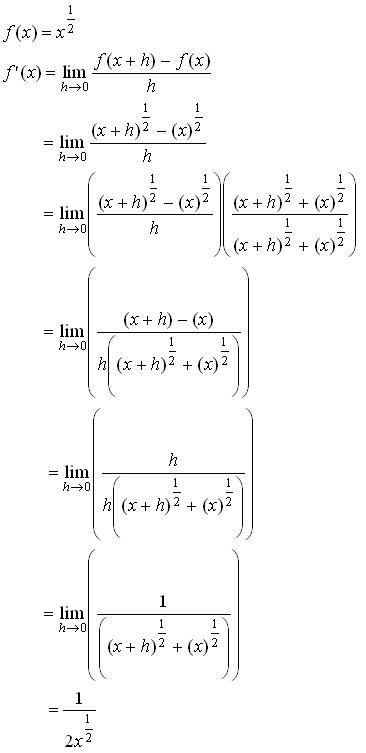
[ Last edited by pipi on 17-8-2004 at 03:09 PM ] |
|
|
|
|
|
|
|
|
|
|
|
 发表于 7-8-2004 12:24 PM
|
显示全部楼层
发表于 7-8-2004 12:24 PM
|
显示全部楼层
y = √x
设 δy, δx 分别为很小的 y, x 变化.
y + δy = √(x + δx)
取左右边的平方,
y^2 + 2yδy + (δy)^2 = x + δx
δy (2y + δy) = δx
δy / δx = 1 / (2y + δy)
当δx, δy 很小时,可以 "abaikan", 而且我们写 δy / δx = dy / dx 得
dy/dx = 1 / 2y = 1 / 2√x .
这是中学 form 4 / 5 时"解释"微积分的方法。当然是不严谨的,不过是一个初步的认识。Pipi 的解答是对,不过本地的中学数学课本都没有解释"derivative"的定义是什么,这种解答恐怕要在form 6 ? 或大学才遇到。 |
|
|
|
|
|
|
|
|
|
| |
 本周最热论坛帖子 本周最热论坛帖子
|