鸟哥数学堂 - 开课咯!!!!!

斷羽鳥

随机性 ＋　决定性 ＋　混沌　＝　多姿多彩的动力世界！
================================================

(注: 由于本帖有一点technical, 希望网友们遇到什么不了解的尽量发问)

看了很多有关数学的贴子, 发现较多的网友都比较热衷于一些普片的数学科目如几何, 代数, 微积分,数学分析等等! [p.s几何, 代数, 微积分并不简单, 只是有些话题总是围绕着入门阶级的, 请别误会我的意思]. 想想也该是时候来些较中等级的讨论啦!!!!!!

其实在这百花齐放的数学领域里还有许许多多,有趣好玩的领域! 有些纯粹就为了好玩,有些却对科技的发展有着举足轻重的相互关系!　动力学就是一个例子！[基本功包含了, 几何, 代数, 微积分等等等等 ...]

今天鸟哥第一堂课, 就先为大家讲讲有关这动力学吧! 拉起八只耳朵听吧! 打瞌睡者, 看帖不回者, 一律杀无赦!!!!! 呵呵呵呵 ... (鸟哥先来个下马威! 骗人的啦, 其实鸟哥我很仁慈地啦)

其实鸟哥我也不知大家的数学指造诣到了个怎样的境界! 所以就随性的选了酱的主题! 希望大家别太介意! 随性听听就好! 听不懂可以问啊!
.
.
.
搞不懂就问人
搞得懂就答人
没有人懂
还可以问神
.
.
.
哈哈! 阿亮唱出了我想说的!

--------------------------------

好! 就有一个大家较少在论坛里谈起的领域开始 - 运动力学!

简单来说宇宙所有物理运动过程, 都可分为两种性质 - 决定性 (deterministic) 与随机性 (stochastic)!

决定性物理动运过程, 就是那过程, 一切都是随着我们明白的物理所进行的! 动向是完全被物理所决定的(由力的牵引), 所以就称之为决定性运动过程!
那么随机性运动过程呢? 一听名称, 大家就想到设么? 随机应变? 机缘巧合? 呵呵! 近了近了, 再猜! 哈哈? 放弃? 英语我们就称它为(随机性)stochastic. 对我来说这是一门挺难的学说! 我就深入浅出的和大家谈谈吧! 有不对的就多多包涵啦!

给些例子大家消化以上'决定性与随机性'运动过程的意识!

打个比方: 我们用力把一个皮球往上抛, 那么皮球的动力物理就是属于决定性的.怎么说呢! 简单, 当皮球离开你手中, 他自然会
受到地心引力的牵引, 掉回地面! 而且一切物理是那么的决定性, 用牛顿定律就可以简单的算出所有的物理变数, 如速度, 路径(trajectory) ... 等等等等!

那么又有哪些物理过程是非决定性而是随机性的呢? 呵呵! 这还不简单, 你赌博难道就不是随机性? 玩大小难道就不是随机?
Hehehe, 如果踢足球马来西亚对垒英格兰, 那我就说是决定性咯! 我买英格兰你和我赌没?  如果说赌博是决定性, 你找鬼和你赌吧! 再来些比较普偏的例子.股市的走势, 早上股市走势强劲, 下午可能就像作过山车酱piuuuuu一下子令你倾家荡产. 反过来也有可能! 呵呵!

对!一切会随着时间而随机改变状况的过程, 就是属于随机性运动过程! 而随着牛顿力学(基本上酱说没错)而改变状况或动向的过程, 就是决定性过程!  

希望以上几个例子可以让大家对决定性和随机性过程有多多少少概念! 比较"数学"上来讲, 决定性过程是能够以牛顿力学微积分来代表或模拟的一种过程! 而随机性过程, 一切都是那么不可预测的, 一切变化都是随着机率(probabilistic)的! 对于这种过程,微积分和一切力学原理就无用武之地咯! 模拟此种过程的, 我们称它为 - 随机模式(stochastic model)! 而它的数学基本就是 - 机率!

-----------------------------------------

如果说世上所有物理都是决定性的, 你说这将会酱啊? 没博可赌, 生活也未免太闷了些吧! 上帝也真是为我们着想哦! 弄了个"随机性" 这东东让我们玩玩!

就当科学家们本以为世上所有物理, 不是决定性就是随机性时, 20世纪初气象学家们领先发现了一样更有趣的东东哦 -  "决定性里的混沌". 这使得人们对于一些过程到底决定性或随机性, 感到模糊! 有些过程, 明明就是决定性的, 怎么偏偏它的动向就是那么难以捉摸, 难以预测呢?

用例子来说明好了! 我们刚才提到! 当我们将物体抛向空中, 物体的动向是决定性, 而且一切力的作用都会符合牛顿定律! 那么如果我们抛得是叶子呢? 就别说用抛的, 试试看把两片一摸一样的叶子, 同样的时间同样的高度, 近距离, 松开手! 你看那两片叶子飘啊飘啊, 伊? 怎么一片飘到东面,一片飘到了你西边屋顶上了! 你不信邪! 再来个实验! 这次你确定你找来了两片一摸一样的 "双胞胎叶子", 你甚至把那两片叶子叠在一起! 松手! oh no ... 一片去了你邻家的屋顶, 一片进了你家的水沟. 怎么啦? 两片一摸一样的叶子, 同个地点同个时间松手! 怎么后来的差距会酱大啊? 而且叶子的动向是酱的难以捉摸, 不可预测! 如果你丢的是皮球, 那这种情况就不会发生! 两者同样有重量, 受同样地心引力牵引 (两者都是决定性的), 为舍么, 前者不可预测, 而后者却可预测呢? 这并不是说叶子的动向是随机性的, 因为基本上它还得跟随牛顿定律移动! 而所有酱子, 难以预测的决定性过程, 我们说它有着混沌的个性 (chaotic behaviour)!   

这使得今天的科学家们更多东东玩喽! "Deterministic Chaos" 这名词对一些着手与流体力学研究的网友来说应该不陌生! 我们来看看到底在舍么情况下会出现酱子的混沌个性?  
  
-------------------------

好吧! 是时候玩玩计算机了! 我们来玩玩模拟! hehehehehe 看看这方程式:
这difference equation 是模拟 population growth, 叫它 logistic equation, 模拟一些生物群的成长过程! 基本上属于一阶运动方程(这下次再讨论)!

A(t+1) = R*A(t)*( 1 - A(t) )
A(t+1) is a function of its previous values at time t. R 呢是 free parameter (可以自由选), 控制着整个方程的性质.

首先让 R=2.0
用 A(0) = 0.123, 那么来算算 A(1), A(2), A(3) .... A(100) ;  A(0) 就叫起点, initial value.

再来用 A(0) = 0.124 为起点, 算算 A(1), A(2), A(3) .... A(100) 又是个舍么样!!!!

[知道你们懒惰不会用手算! 呵呵, 所以给你们做了个小小方便的计算器! http://juneng.port5.com/cari/logistic.htm ,怎样?鸟哥我还算仁慈吧]

看到了吧,  就算起点有一点偏差, 但最后我们还是可以知道数值最后还是会停留在 4.99999999. 那 A(101) 是舍么? 当然是 4.99999999 咯! 不信你就算算看楼! 就算起点有些偏差, 但他们俩的trajectory还是会慢慢被引到 4.99999999 (我们称这解为attractor, 可以叫它, singularity(所谓single就是单一) 因为trajectory被吸到一个点).这种过程不难预测吧!


来看看些有趣的! 让 R=3.3  用同样的两个起点, A(0) = 0.123 和 A(0) = 0.124.  

解是:
0.4794270198
0.8236032832

就算起点有一点差距, 它们的解还是会在0.4794270198 和 0.8236032832 间摆荡!  不是0.4794270198 就是0.8236032832, 0.4794270198 过后就是 0.8236032832, 0.8236032832 过后就是 0.4794270198. 绝对可预测! 那么这个attractor 是一种oscillator(在两个数值之间摆动). (两个点的oscillator). 虽然起点偏差, 但trajectory到后来也还会被引到一起, 在那两点摆荡. 这种过程也不难预测吧!!

来句英语: the charactetistic of  both the systems are well-behaved or we can say that the systems are tame.

再来看看些更有趣的! 现在让 R=3.8  再用同样的两个起点, A(0) = 0.123 和 A(0) = 0.124.
解是? ...??????? 呵呵!!!!有舍么不对吗?  有趣的事情发生咯!! 对吗?

当 R=3.8 怪事发生了, 起点有一点偏差, 会造成两个iteration trajectory 的差距越来越来离谱哦! 如果现在要你预测A(101)是舍么?　难吧！(如果你不是事先知道那是logistic equation, 更不知道, 控制那方程式的parameter是舍么. 要预测这种过程似乎就要考考你的本事了!  [不信我们也可以来个比赛, 我用那logistic equation, generate 出100个值, 让你们去测出第101个值!]

看到了吧　当R=2.0，那logistic equation的特性还是可预测的　，当一旦　R=3.8,　他就呈现它那不规矩的一面　－－　混沌的特性！

但这3者都是决定性的！基本上我们还是可以通过那方程式找出　 A(101) 是舍么！只是稍微起点的一点偏差就会带个你十万八千里差距的 A(101) 值！你会问那R=3.8的时候, 还有attractor 吗? 答:有! 只是那attractor不是,singularity, 也不是, oscillator.夷!... 呵呵 ... 我知道有人想说 "我知道, 我知道了".

对!那就是, strange attractor. 有着分形 (fractal) 的性质, 有着非整数的dimension(比如我们生活在3D世界,是属于整数的.). 这就不谈了.
科学家坛主写有一篇关于分形的文章 ... 在这: http://chinese.cari.com.my/myfor ... ge=1&sid=zMuVlC

由以上, 我们可以看出, 那logistic equation的特性是由哪 R parameter 控制的, 当 R 越来越大, 那整个过程会慢慢越来越不规矩! 问题是, R=?? 的时候, 那strange attractor才真正出现? 整个系统才变得chaos(混沌)呢? 不告诉你, 等你心兮兮! 自己研究吧! 都作了个计算器给你咯!

大家可以研究研究, R=? 的时候, 你会找到 4个, 8个, 16个 ... 点的oscillator solution. 是不是当 R 越变变大, 那oscillator attractor 点就会以 2^n 的速度快速增加?

这种现象我们称之为 bifurcation (分叉的意识). 这种, 由singularity, 然后分叉进而变得混沌, 我们称为, "bifurcation route to deterministic chaos" (从一个变成两个,两个变成四个…)
不说了, 其他的就由你们自己温习吧!

值得一提的是, 很多时候, 学者们都不太清楚, 一项运动过程是 "混沌, 决定性" 还是完完全全随机性. 举个例子, 股票走势动荡!
在经济研究领域有两个学派各个分别自持两个假设学说:

1. efficient market hypothesis.(股票走势动荡 -随机)
2. coherent market hypothesis. (股票走势动荡 -混沌, 决定性)

相信那一个? 呵呵...我嘛?.... 呵呵...我相信TIPS. 哈哈哈 ...

还挺累人的叻! 没人顶我不写了哦!

发现一样东西！ 科学论坛的网友大都比较拘谨！ 不太会开玩笑！ 别酱嘛！ 来笑一个！ 科学应该是一个好玩， 有趣的东东， 为世界带来欢笑绝对比为它带来最先进的科技重要！个人想法, 玩玩就好，玩玩就好， 别太认真！ 没人读过我的苹果哲学吗？

如果想称赞我几句， 可以在这回帖. 觉得鸟哥我臭屁, 想骂我， 升我一脚者， 请pm. 但不可以说我妈妈， 不可以讲我丑, 不可谈生*器, .... 呵呵呵呵呵　．．．！

下期你们想听我用数学教你们谈恋爱还是想我教你们上云顶赌博啊?????

参考：
http://hypertextbook.com/chaos/42.shtml

鸟哥我要多谢微中子老第帮我改这改那的!!!!!

[ Last edited by 斷羽鳥 on 16-3-2004 at 09:50 PM ]

顶顶顶顶顶..........断羽兄....加油........

上你的课啊.....
很轻松很有趣.......

不过......
就辛苦你了.......
得为我们搜查资料....

谢谢你的课....

斷羽鳥

先谢了! 开这课的目的是, 可以和大家来讨论些比较另类的课题! 分享一部分我的知识, 让大家试着接触着一些比较应用方面的数学, 如你们有些舍麽特别的数学领域要我说说的就回帖通知我吧! 办到的, 我一定会给大家上这课的!!!!

[微中子: 数学比赛+10分]

[ Last edited by 微中子 on 11-7-2004 at 11:09 AM ]

flyingfish

谢谢断老师,太好看了..
那参考"书"蛮好看的,暂时看到bifurcation那里(很慢)..觉得那图蛮有学问的..
想问问stochastics的应用,和如何用..

"复杂学"的历史进程是不是如以下网上所说:
http://www.exploratorium.edu/complexity/slider.html

glossary:
http://www.exploratorium.edu/complexity/CompLexicon.html

[ Last edited by flyingfish on 17-3-2004 at 11:10 PM ]

斷羽鳥

哎哟! 叫我老师太沉重呢! ... 叫鸟哥吧!!!! ...

谢谢飞鱼的两个link, 我看了! ...哇塞! 勾起了我无数的回忆! 那些人名, 曾几何时, 简直就是鸟哥我的偶像! ... 来来! 先列出鸟哥我比较熟悉的! ...

Andrei Kolmogorov - 对随机学有不可漠视的贡献!
Edward Lorenz - 气象学家, 简至就是鸟哥我的偶像!
Alan Turing - 这位嘛? 念电脑的不可能不知, 可以说是电脑之父! 不过性生活有点不检点! 英年早逝, 基老一名!
Benoit Mandelbrot - 50-60年带, IBM红牌researcher, 对分形发展有着很大的共献! ... mandelbrot set 就是由他带出!
Michele Henon - deterministic chaos, 一个最常用到的列子就是Henon system (henon map)
Poincare - 拓扑学之父! 与爱因斯坦, 亦师亦友! 没有他就没今天你们知道的 - 相对论! 既然说到他, 就来谈谈这吧!

想请问有谁知道相对论的数学基本，有一大部分是，拓扑学（topology)，而拓扑学就是以Theory Set为基本而建立起来的呢？而Theory Set 和 Logic 和数论又是那么习习相关的??

拓扑学可以说是相对论的副产品! 拓扑学的存在, 就是为了要作为相对论的基础! 如果有人硬要把"爱因斯坦的相对论"说成是"Poincare的相对论", 我想我不会反对的! ... 也顺便提提, 他发明的poincare section是一个管范被利用的一种数学工具!

其他的人我就不太熟悉了!

其实, 那篇文章是鸟哥我凭着记忆, 骗吃骗吃写出来的 ... 看了那些link, 还真有些怀念过去那! ... (鸟哥我退出数学界好久啦) ... 还真是忘了好多东西没提到那! 如果你们有东东要讨论的, 那鸟哥我就尽量少喝点酒,少抽点烟, 让记忆快点恢复好了!

好像少了几个重要的人物: ... 以下列出:
Gaston Maurice Julia
还有... 派谢 ... ... 想不起来!

julia最为人知道的贡献就是发现julia set, mandelbrot set 的complement!

来看看一mandebrot/julia set 是个舍麽样!
mandelbrot set

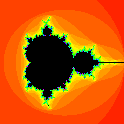
julia set



有关祥情请看连接:
http://aleph0.clarku.edu/~djoyce/julia/julia.html

鸟哥我就不讲了啊, 乖! (其实是鸟哥我自己忘了一大半, 呵呵 ...)

其实, complexity  这词嘛, 不是指复杂学啦, 听起来怪怪 ...
complexity, 只是一个general的说法! 一个system, 如果由很多个free parameter所操控, 哪它"可能"就很复杂, 我们说 the system is complex, 有时候, 有人说, the problem is ill-posed. 有没"复杂学"这名词, 鸟哥我就真的不懂咯!!!

[ Last edited by 斷羽鳥 on 18-3-2004 at 12:26 AM ]

斷羽鳥

有关随机学! 鸟哥我会为你们介绍一种 随机模式(stochastic model) - 马尔科夫连! (markov chain). 然后带你们上云顶找林伯伯去!!!!!!! 哈哈 .... 敬请留意咯 ...

[ Last edited by 斷羽鳥 on 18-3-2004 at 12:31 AM ]

agsd121

随便写几句..
A(t+1) = R*A(t)*( 1 - A(t) )的一些特性可以用它的dimensional map分析出来..几围就看变量在里头等等了.

早期计算机里的random number generator,Von Neumann 用的是x[n+1]=4x[n](1- (x[n])

当分析fractals时用了许多affine transforms,metric space,contraction mapping等类的东西. deterministic algorithm与Random IFS是很常用的算法来看fractals..

[ Last edited by agsd121 on 18-3-2004 at 01:45 AM ]

斷羽鳥

谢谢! agsd121的分享!


照阿! 怎么鸟哥我忘了还有Neuman啊? ... 对于game theory的贡献是世人不能忘记的!
如果谁对schrodingerwave 和heisenberg's Matrix 有研究, 这名字, jon von Neuman, 应该不会陌生! 在零零星星的影像中, neuman 好像只提议了可以用那logistic equation来generator random number, 但好像真正如此做的是别人也!祥情是怎样的! 鸟哥我也真是不懂了!

不过鸟哥我猜想, 这肯定是行的通的啦. 还请agsd121副上解说, 或一些links. 如果大家想要了解多一点关于如何用那 logistic equation 来generate random number, 可以自己找找看google啊, 乖自己自修啊! 鸟哥没空 (其实是鸟哥我也不会 ...呵呵).

但鸟哥很希望有人可以自修了再告诉我, 用logistic A(n)=4A(n-1)(1-A(n-1))可以generate出舍麽distribution的random number. okay? 这鸟哥我很有兴趣知道.

说道random number就得说pseudo-random number generator. 舍麽东东嘛这? 哇老! 鸟哥我又说又远了! ... 自己自修咯然后出来这和大家说说 random number generator 和 pseudo-random number generator 的关系! okay ... 搞不就问人, 搞得懂就答人 ..., 如果没人告诉我, 鸟哥我过多几天去拜神问问看!


affine transforms,metric space和contraction mapping  ...这几样东西嘛! ... emmm ... well鸟哥我还是跳过吧! ... 误人子弟这罪名还真当担不起! ... 都怪鸟哥我喝了酒 ... 酒精作怪,想不起点头绪 ... 都怪就酒精作祟 ... 呵呵 ... [借酒好下台] ...

well, deterministic 和 random iterated function system, emmmmm ... 这我懂, 但要怎样才能简单的介绍给大家呢 ... well well ... emmmm ... 哈哈 ...   试试看吧! 别见笑哦.

well, deterministic algorithm不是一种algorithm (algorithm大家应该知道是舍麽吧??) 的名称! 它是一种algorithm 的特性 (behaviour)!

          algorithm
input --------------> output

如果只给你input, 这algorithm 的 behaviour可以完完全全由那 input 来预知! 哪这alogoritm的特性就是 deterministic的! 酱说你们明白吗? ...不明白是嘛 ... 酱我也不用解释  random iterated function system 咯 ??? 哈哈 ... 过关! well, 鸟哥我也不知怎样简单的解释也 ... ! 简单来说, 这两样工具可以画出各式各样的分形图案!

放过我一马吧! ... 求求你啦! 我想还是交给比较懂的 agsd121 来说吧! ... 就麻烦 agsd121 咯!

或是有谁自修了的想出来分享的 ... 鸟哥欢迎!

哟! 我不懂的还真多哦! ... 可能是和鸟哥我这种得过且过, 能混口饭吃就好的个性有关吧! ... 不过还是要劝各位, 以上这些名词可以慢慢来明白, 不用急啦!
是属于比较intermediate的课程(是鸟哥我的个人认为). 如果你要现在明白也可以啦! ... 但凡想破脑者, 凄线者, 鸟哥我一概不负者! 哈哈! ...

还请 agsd121 出来说说! 你应该是修电脑或物理的吧????????

就酱!

[ Last edited by 斷羽鳥 on 18-3-2004 at 04:40 AM ]

斷羽鳥

发现好料！

http://www.phil.pku.edu.cn/perso ... art/html/notice.htm

有关分形！ 全华语的哦

胤

你这些数学是什么程度?
前面的还明白
但后面的完全不明白

斷羽鳥

这应该是大一或大二的程度! 对不起! 可能后面越说兴起, 说难了! ... 没关系, 最主要的目的是要告诉你们, 所有运动物理过程可分为那3种! ... 了解到这点就应该不错了! ... 其他就要自己自修了. 我的程度不够教你们了!

斷羽鳥

阿爸说1+1=2，　阿妈说1+1=2，　姐姐说1+1=2，　老师说1+1=2　所以　1+1=2　？？？
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

哎哟哟!  鸟哥数学堂第一课好像没舍麽人问津. 生意难做 … 所以鸟哥我决定降低水准, 说些你们可以只用4只耳朵听懂的课就好! … 再不懂那只好降低到2只耳朵咯! 就把那”恋爱方程式”和 “去云顶赢钱”的计划压后吧! 毕竟谈恋爱, 赌钱, 都是大人的玩意儿, 我们小孩子来玩 1, 2, 3 就好!  (注:大一程度[Real Analysis课程])

看到很多人对那1+1=2的帖子感兴趣. 鸟哥我决定抢生意咯! … 呵呵呵!  … 不好意事呢!

事先声明! 鸟哥我不是要证明1+1=2. 而是告诉你为舍麽 1+1=2. 别搞错咯! … 以鸟哥我今时今日的智慧, 想要完完全全证明1+1=2, 还需等500年, 吃１000包的米才行呢! (鸟哥我以经很努力在吃, 但很多人还是讲我 ”贾料米”呢, 不懂为虾米呢?)

想要知道为舍麽1+1=2, 我们需要建立起一个公理体系(axiomatic system)! 和几个definitions.

公理体系
=======
首先先来弄明白舍麽是 axiom, definition, theorem, corollary! 以下鸟哥我把记载在  http://www.math.hkbu.edu.hk/~wllee/maths/maths_concept.html 的一部分内容给paste上. 不多做解释! ... 又解释又乱, 因为鸟哥我华语表达能力有限哦!

==========================================================================================
公理(axiom):不加證明而可作推理依據的真實命題。
定義(definition):用以揭示概念的本質屬性的命題。
定理(theorem):經過証明後方可作為推理依據的真實命題。
推論(corollary):証明某定理後稍加思索便可確定的定理。


作為公理系統要滿足三點要求:
(1) 相容性----即各公理之間不存在互相矛盾的現象。
(2) 獨立性----即要求公理的條數量的少，就是不要有能被其他公理可証明。
(3) 完整性----即由定義和公理組成的公理系統，能保證不必借助直觀而純粹邏輯推理的方法展開全部幾何學。
===========================================================================================


如果我说所有的的科学理论都是'骗人'的! 你会说我吹水吗? 可能会用鸡蛋丢我吧? 难道几百年来牛顿定律是骗人, 爱因斯坦的相对论在吹水? 咳呀! 我又没说全部理论是错, 只是不能被100%证明是对的. 听我说嘛! 酱激动干嘛? 难道鸟哥我会点条黑路你行么? 误人子弟这罪名我可担当不起啊! 酱子说大多数科学家都会同意的, 因为基本上我们所有的理论都是建立在公理体系上, 只有完美与不完美! 没有对与错! 何为公里? 所有的logical proposition, 如果”思想”上完完全全是没错的, 但就是不能以逻辑证实是对的, 我们就可把它设为公理! 英语叫它: axiom 或 postulations

用例子说明最简单!
"0 是一个自然数" 谁可以证明给我看这logical proposition 是对的？或错的？ 100% 不能， 没有人可以证明的！ 不信你试试咯！一切后果，如脑抽筋，脱线变白痴，心里变态不平衡，鸟哥我一概不负责！所有的理论，包刮数论， 都是由这种完全”没错＂但不能被证明对的公理所建立起来！想要明白更多，或者不明白鸟哥我所说，又或者不信我，说我吹水，可以看看这篇文章：
<<任何理论都不能被证明是“对”的>> - http://yangzhizhu.com/xiezshidui.htm

数论入门第一阶，第一级，第一科，第一本，第一章，第一页，第一招，第一式： Peano 公理！（注：不是钢琴， piano, 写错者! 斩!)
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
Well, 通常数论, 第一堂课老师都在教舍麽啊? - 自然数! 别告诉我你不懂虾米是自然数! 鸟哥我翻脸纳! ...咳..没法啦, 谁叫我太仁慈了. 不懂看这儿! 自然数是数论的最基本! 数字本来就是一个体系 - 一个公理体系.

问:虾米? 数字不就是 1 2 3 4, 2 2 3 4, 3 2 3 4, ...吗？　
答:靠! 弟弟仔 ... 你来错地方了啦 ... 应该去这啦 ... 乖!

对!是一个公理体系! Bingo! 猜对了, 作为基本, 建立起整个自然数体系的就是 Peano 公理! 由5个”思想” (axioms)所组成. 也有人说是13个, 但其实最基本只有5个, 其他八个都是由那5个所演变而成! 所有数论的理论都得依靠这五个公理来"生存", 来验证! 如果有一天你发现进而证明其中一个是错的,那恭喜你,下一个诺贝尔奖得主肯定就是你, 整个数学体系, 历史, 将要改写!

下列我把全英语的给paste上.

5个最基本的Peano's axiom.
========================
A1. Zero is a number.
A2. If a is a number, the successor of a is a number. (equivalent to say, every number has a successor)
A3. zero is not the successor of a number.
A4. Two numbers of which the successors are equal are themselves equal.
A5. (induction axiom.) If a set S of numbers contains zero and also the successor of every number in S, then every number is in S.
======================================================================================
**不好意属啦, 鸟哥我华语不好啦, 哈瞒想翻译就请帮帮忙啦!

以上英语写成的好像不太好明白哦! 别担心啦, 一位数学家随时可以变把戏,用数字写出那五句英语写成的axioms. 连"女人=恶魔" 都可以证明了, 还有虾米可以难倒那些数学家们对吧?[注: 鸟哥呱不是数学家, 呱是上网学家 - 上网最厉害]

下列用比较数学的方法写出那5个Peano's axiom.

A1. 0 是一个自然数.
A2. 如果 a 是自然数, 那 a + 1 也是自然数. [注: + 这 operator, 再这5个公理之前是不存在的, successor=后继]
A3. 没有一个自然数加了1之后会等于0的.
A4. 如果a+1=b+1, 那么, a=b.
A5. 如果你能证明 a ∈S 的一些property, 再证明 a+1 ∈S 拥有同样的 properties, 那么所有 k∈S 都拥有这property (这可能较难明白, 基本上, 这就是所说的 - mathematical induction). 所以A5. 就是mathematical induction 的由来! 注: 这和上面英语版的格式上有点不同但意识完完全全一样地! … 以鸟头担保! (好彩我不是叫 … 忍者龟舍麽舍麽的 … 要不然 … 我可不敢用我的头作担保! 呵呵 …)


还有更数学的翻译，这就不讲了（需要８只耳朵的，　完全没有一个英文字的，都是Greek 蝌蚪字, 如果真的有人有兴趣想看懂这些蝌蚪字, 告诉我, 我们改天再聊聊）



注:以上的蝌蚪字axiom是以 1 做为开始, 不是 0. 但都一样啦!
自己看吧！厉害吧? 把原先的白化文完完全全数学化！"女人=恶魔"　赫，sup sup water 啦！　

这五个axiom还不足以建立起整个数字体系, 我们还需要些补助的 definition. 我只讲一个, 因为我等下会用到啦. 其他的definition, 你们自己, 温习啊! 乖!
看这: http://hemsidor.torget.se/users/m/mauritz/math/num/nataritm.htm

我要define的这东东就是 operator +
=========================================
+ 是一个 binary operator, 拥有以下的特点:-

如果 a ∈S, S 里将有一个特别elemnt, 0 使到 a+0=0+a=a
在你define + 的set里, 会有一个element, b 使到 a + b = b + a = 0, 意思就是, 不管你加给a舍麽你都可以收回!
+ 会有两种个性
   i) associative, 就是如果 S(a) 是a的successor, a+S(b)=S(a+b), 如不明白, 就是 a+(b+1) = (a+b) + 1
   ii) commutative 就是 a + b = b + a
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
还有其他的operator就由你们自己自修吧, 也可以拿来这讨论! (减, 乘, 除 ???）


现在我们已经有足够的工具来了解为舍麽　1+1=2　了．来来来, 现在我们来看看怎样从这五个公理和那 + operator 来找出1+1=2．

虽然你会认为很费, 弟弟仔, 这才是数学! 真正的数学! 不想听就到这儿玩吧! ... 乖!

有时候我想, 数学是一个很累人的东西, 得把一些普通人看得懂的东西, 变为他们看不懂,而我们自己看得懂，才能够做reasoning, 很多时候, 数学家们就酱子被人们误解为疯子, 或是对科技发展没有贡献的一群! 可怜! 你们可知美国每年有一笔数目不小的军事研究基金去了哪儿？猜猜吧！发展基本纯数学的一路上才能开发出应用数学领域！别忘了这点！没有任何学问应被视为废物！鸟哥我虽然每天得过且过，浑浑噩噩过日子，但对这点，我的立场是绝对的！．．．绝对尊重所有学问(包括我不太明白的神学！)

来咯! 唔好眨眼啊! ...

0 是自然数! (A1)
define S(k) as the successor of k. Hence S(0) = 1, S(1) = 2, S(2) = 3 ... 等等!　
从＋的definition，　我们有：
a+0=a
a+S(b) = S(a+b)　－－－－（１）

让　a = 1, b = 0，(1)　给我们带来
1+S(0) = S(1+0), 我们知道S(0) = １（刚刚才define的）, 和刚才刚刚说到的+的第一个个性　
a + 0 = 0
=>　1+0=1
=>　1+1 = S(1)
=>　1+1 = 2　（塔拉．．．）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

问大家一句，我们是不是已经完完全全的'求证'　１＋１＝２？没！基本上1+1=2，不能从根本被求证，别忘了，我们必须以那Peano公理为基础，再来得definine ＋（其实那＋的definition也是以Peano Axioms为基），才可以带出　１＋１＝２．严格上来说，这不是求证，１＋１＝２只不过是以Peano Axiom为基的一个DEFINITION吧了！现在还有许多数学家想尽办法求证１＋１＝２．　但大多必须用其他　Axioms／postulation　或　conjecture 为基！然后通过logical reasoning　来带出１＋１＝２．所以这种证题, 并不100%完整／完美!

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

呵呵！　看到了吧？这就是数学的真面目！如果你们以为的数学就是那几个难难得舍麽e=mc^2，光束绝对，黑洞白洞！gravity＝舍麽舍麽地！那我可以告诉你们，想要明白相对论的根本(但你们可能明白它的物理，但绝对不是它的数学），你们好像跑错了路线．想请问有谁知道相对论的数学基本，有一大部分是，拓扑学（topology)，而拓扑学就是以Theory Set为基本而建立起来的呢？而Theory Set 和 Logic 和数论又是那么习习相关的! 随便在google里找找: relativity +topolgy, quantum theory +topology. 看看得到了舍麽? 如果打开一本Quantum theory的课本, 里面满满都是, theorem, axioms, definition, preposition. 那才是一本教你Quantum theory '基本'数学的书!

唉哟! 怎么严肃起来了! 呵呵 ... 不好意是 ... 可能因为天气冷 ... 呼 ... 是时候来根烟啦唯! 再来杯咖啡 ... 哈哈! 不懂你们懂没, 咖啡可是很多科学家们的精力与灵感来源呢! 　


嘻嘻 … 鸟哥变态问答没奖游戏来咯!

问: 请 'show me '  2 > 1
没有对与错, 只有完美与不完美, 来!让鸟哥我看看你们脑里装的是设麽!


参考:

http://www.matran.de/matran_files/matran4_files/essay02.htm
http://www.cut-the-knot.org/do_you_know/addition.shtml#axioms
http://www.engr.iupui.edu/~orr/w ... athbios/gepeano.htm　（介绍GIUSEPPE PEANO）

[ Last edited by 斷羽鳥 on 25-3-2004 at 09:57 PM ]

flyingfish

斷羽鳥 于 18-3-2004 00:24  说 :
哎哟! 叫我老师太沉重呢! ... 叫鸟哥吧!!!! ...

谢谢飞鱼的两个link, 我看了! ...哇塞! 勾起了我无数的回忆! 那些人名, 曾几何时, 简直就是鸟哥我的偶像! ... 来来! 先列出鸟哥我比较熟悉的! ...

Andrei K ...

在"书虫"论坛那里,看到这Ebook 的网站有"复杂"这本书:
http://read.ah165.net/3hsj-7.htm

毅承

鸟哥，您可不可以为我们讲解game theory吗？目前我读到有点一知半解，我想彻底了解。

谢啦！

微中子

哇。。。

三年前的帖子！

chan1314

我也奇怪看到鸟哥在这里出现， 原来那么多年了。

想不到这个 linux 高手数学造诣非凡。 去linux 区请他回来咯。。。

~HeBe~_@

原来已久沉帖的帖子出来了。。。
鸟哥先辈。。。。很高兴可以看到这帖。。
可能我要请教你了。。
下学期将会在operations research学game theory。。。

mad1427

请问A(t+1) = R*A(t)*( 1 - A(t) )里的*代表什么。。。？要怎样决定A（０）的值。。。？

斷羽鳥

原帖由 mad1427 于 25-10-2007 09:29 AM 发表
请问A(t+1) = R*A(t)*( 1 - A(t) )里的*代表什么。。。？要怎样决定A（０）的值。。。？

Hooooooolweeeeee shit ... 什么时候跑上来 ... 不要叫我高手. 很沉重!

ooooi ... 大家可好呗! 离开数学好久鲁 ... 不是我放弃, 而是我改变了我对数学的方向. 认为是时候运用数学, 对人民, 对自己有所贡献了. 这几年,我不断用数学方法,改进/研究关于大气/海洋物理,以便了解更多关于气候还有它的短期可预报性,希望可以减低灾害带来的伤害. 不过有空还是会回来看看的. 今天就看到很多数学爱好者 ... 欣慰下. I can assure you ... 你们的选择是"对的"!




阿mad, 你那是 logistic equation, 是个 difference equation. A(0) 自己定啊. depend on your R, 这整个方程系统混沌特征, 可能不会.

黄大铭

你也有精华帖啊？
这样你已经成水仙叻